Примерный тест для зачёта. Решение Пусть решение системы. Тогда выражение равно а 1 б 2 в 3 г 0 д 1 Решение
 Скачать 79.87 Kb. Скачать 79.87 Kb.
|
|
Тест по алгебре и геометрии (ИИН, 2022) Определитель 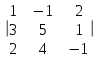 равен: а) 10; б) -10; в) 8; г) -1; д) 0 равен: а) 10; б) -10; в) 8; г) -1; д) 0Решение 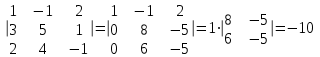 Пусть 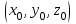 решение системы решение системы 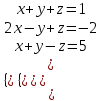 . Тогда выражение . Тогда выражение 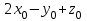 равно: равно: а) 1; б) -2; в) 3; г) 0; д) -1 Решение Складывая второе и третье уравнения системы, получаем 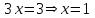 . . Складывая первое и второе уравнения системы, получаем 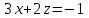 . Следовательно, . Следовательно, 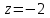 . Из первого уравнения получаем . Из первого уравнения получаем 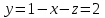 Прямые 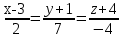 и и 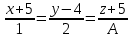 перпендикулярны, если перпендикулярны, если 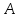 равно: равно: а) -2: б) 3; в) 1; г)2; д) 4 Решение Если прямые перпендикулярны, то и их направляющие векторы также перпендикулярны. Значит, скалярное произведение направляющих векторов равно нулю. Откуда получаем 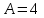 4. Векторным произведением векторов 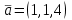 и и 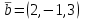 является вектор с координатами: является вектор с координатами:а) 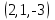 ; б) ; б) 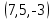 ; в) ; в) 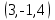 ; г) ; г) 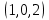 ; д) ; д) 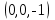 . . Решение 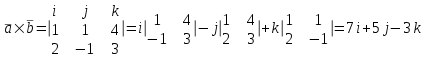 5. Дайте определение собственного вектора и собственного значения матрицы линейного оператора Решение Пусть 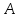 – линейный оператор, заданный квадратной матрицей – линейный оператор, заданный квадратной матрицей 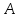 . Если существует ненулевой вектор . Если существует ненулевой вектор 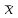 и такое число и такое число 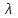 , что , что 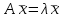 , , то число 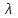 и вектор и вектор 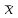 называются соответственно собственным числом (собственным значением) и собственным вектором оператора называются соответственно собственным числом (собственным значением) и собственным вектором оператора 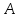 (матрицы (матрицы 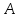 ) )6. Напишите каноническое уравнение эллипса Решение 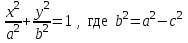 , , где 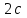 - расстояние между фокусами. - расстояние между фокусами.7. Выберете правильное продолжение определения скалярного произведения векторов. Если угол между векторами 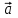 и и 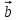 равен равен 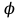 , то скалярным произведением этих векторов называется , то скалярным произведением этих векторов называется а) число, равное 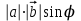 ; б) число, равное ; б) число, равное 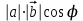 ; в) вектор, длина которого равна ; в) вектор, длина которого равна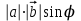 ; г) вектор, длина которого равна ; г) вектор, длина которого равна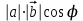 ; д) нет правильного продолжения. ; д) нет правильного продолжения.8. Вычислите скалярное произведение векторов 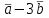 и и 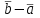 , если , если 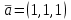 и и 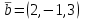 Решение 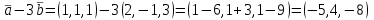 Аналогично, 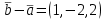 . . Следовательно, 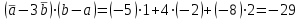 . . 9. Плоскости 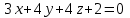 и и 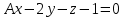 перпендикулярны, если перпендикулярны, если 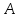 равно: равно: а) -2: б) -3; в) 1; г)2; д) 4 Решение 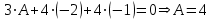 10. Прямая 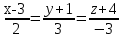 и плоскость и плоскость 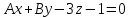 перпендикулярны, если произведение перпендикулярны, если произведение 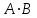 равно: равно: а) 3: б) -3; в) 1; г)2; д) 6 11. Дайте геометрическое определение гиперболы и напишите её каноническое уравнение Гиперболой называется геометрическое место точек на плоскости, для которых модуль разности от двух фиксированных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами. 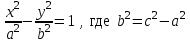 12. Какая поверхность называется цилиндрической. Что такое направляющая и образующая цилиндрической поверхности. Пусть в пространстве задана кривая  и прямая и прямая  . Через каждую точку линии . Через каждую точку линии 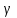 проведём прямую, параллельную прямой проведём прямую, параллельную прямой 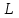 . Поверхность, получаемая в результате такого построения, называется цилиндрической. Линия . Поверхность, получаемая в результате такого построения, называется цилиндрической. Линия 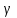 называется направляющей, а построенные прямые – образующими цилиндрической поверхности. называется направляющей, а построенные прямые – образующими цилиндрической поверхности.13. Рангом матрицы называется: а) любой минор этой матрицы, не равный нулю; б) наименьший порядок минора этой матрицы, не равного нулю; в) наибольший порядок минора этой матрицы, не равного нулю; г) наибольший порядок минора этой матрицы, равного нулю; д) наибольший минор этой матрицы |
