ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 1 из 32

ФУНКЦИИ

Тема 1. Функции

1.1.Основные элементарные функции и их свойства

Постоянной величиной называется величина, сохраняющая одно и то же значение. Например, отношение длины окружности к ее диаметру есть постоянная величина, равная числу  .

Если величина сохраняет постоянное значение лишь в условиях данного процесса, то в этом случае она называется параметром.

Переменной называется величина, которая может принимать различные числовые значения. Например, при равномерном движении s = vt,где путь s и время t — переменные величины, а скорость v — параметр.

Если каждому значению х множества Х (х ∈X) ∈ ставится в соответствие вполне определенное значение у множества Y (y ∈ Y), то говорят, что на множестве X задана функция у = f (x).

При этом х называется независимой переменной (или аргументом), у — зависимой переменной,а буква f обозначает закон соответствия.

Множество X называется областью определения (или существования)функции, а множество Y — областью значений функции.

Способы задания функции. Существует несколько способов задания функции.

а) Аналитический способ,если функция задана формулой вида у = f (x). Этот способ наиболее часто встречается на практике. Так, функция   задана аналитически.

б) Табличный способ состоит в том, что функция задается в виде таблицы, содержащей значения аргумента х и соответствующие значения функции f (x),например, таблица логарифмов.

в) Графический способ состоит в изображении графика функции — множества точек (х, у)плоскости, абсциссы которых есть значения аргумента х,а ординаты — соответствующие им значения функции у = f (x).

г) Словесный способ,если функция описывается правилом ее составления, например, функция Дирихле: f (x)=1, если х рационально; f (x) =0, если х иррационально.

Функция может быть задана программой,вычисляющей ее значения с помощью компьютера.

Основные свойства функций.

1. Четность и нечетность.Функция у = f (х) называется четной,если для любых значений х из области определения f (-x)= f (x),и нечетной,если f (-x)= -f (x). В противном случае функция у = f (x)называется функцией общего вида.

График четной функции симметричен относительно оси ординат, а график нечетной функции — относительно начала координат.

Например, у = х² -четная функция (см. рис. 2. 3), у = х³ — нечетная (см. рис. 2. 2), у = х² + х³ — функция общего вида (ибо f (-x)≠ ±f (x),т. е. (- х)² + (-х)³ ≠ ±(х² + х³).

2. Монотонность.Функция у = f (x)называется возрастающей (убывающей)па промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

Пусть х₁, х₂ ∈X и х₂ > x₁.Тогда функция возрастает на промежутке X, если f (х₂) > f (x₁),и убывает, если f (х₂) < f (x₁).

Функции возрастающие и убывающие называются монотоннымифункциями.

Так, например, функция у = х² (см. рис. 2. 3) при х ∈(- ; 0] убывает и при х ∈[0; + ) возрастает.

3. Ограниченность. Функция f (x) называется ограниченной на промежутке X, если существует такое положительное число М > 0, что |f (х)|≤ М для любого х ∈X. Впротивном случае функция называется неограниченной.

Например, функция у = sin x (см. рис. 2. 10) ограничена на всей числовой оси, ибо |sin x| ≤ 1 для любого х ∈ R.

4. Периодичность.Функция у = f (x) называется периодической с периодом T ≠ 0, если для любых х из области определения функции f (x + T) = f (x).

Например, функция у = sin x (см. рис. 2. 10) имеет период Т =2p, так как для любых х sin (x + 2 )=sin x.

В табл. 2. 2 приводятся основные элементарные функции, их основные свойства и графики.

Таблица 2.2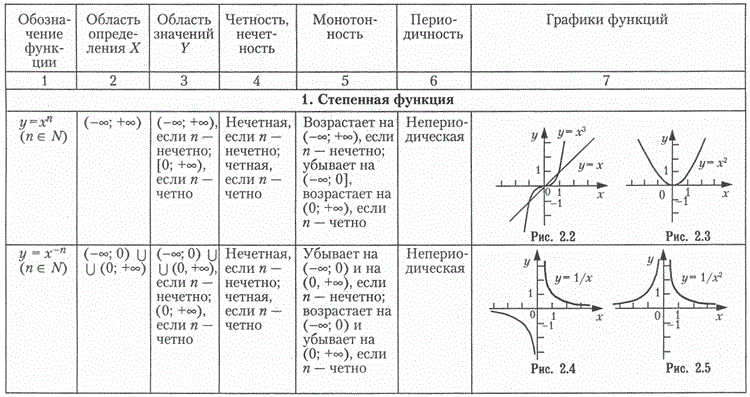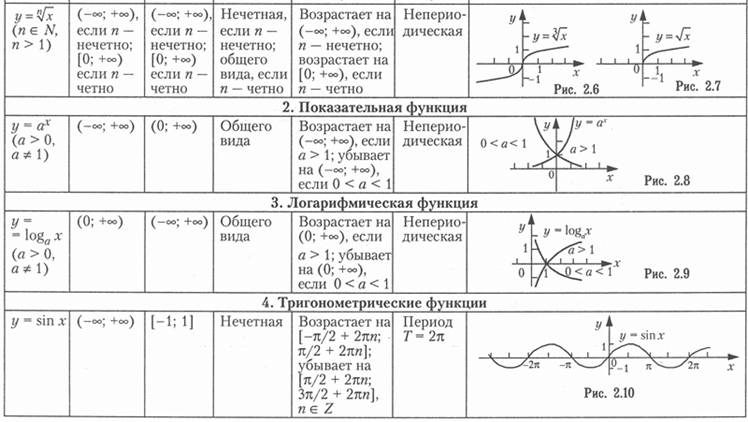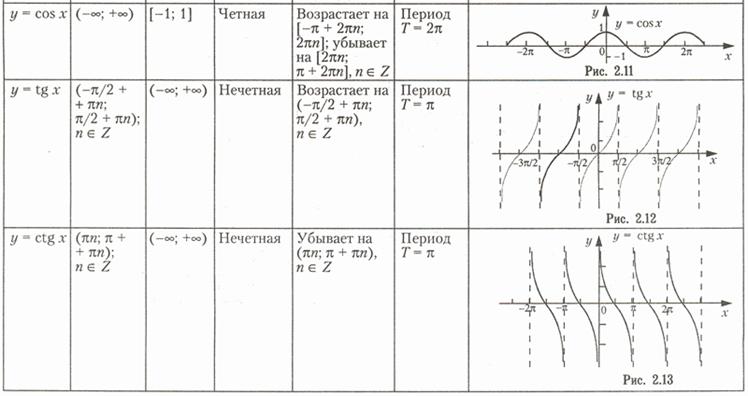









1.2. Функции в экономике. Преобразование графиков.

Функция называется явной,если она задана формулой y = f (x),в которой правая часть не содержит зависимой переменной; например функция у = х² + 5х + 1.

Функция у аргумента х называется неявной,если она задана уравнением F (х, у)=0, не разрешенным относительно зависимой переменной. Например, функция у (у ≥ 0), заданная уравнением х³ + у² - х =0.

Обратная функция. Пусть у = f (x) есть функция от независимой переменной х, определенной на множестве X с областью значений Y. Поставим в соответствие каждому у ∈Y единственное значение х ∈X, при котором f (х) = у.

Тогда полученная функция х = j (y), определенная на множестве Y с областью значений X, называется обратной.

Для любой строго монотонной функции у = j (х) существует обратная функция.

Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 2. 18 показаны графики взаимно обратных функций у = а^хи у =log_a . x при а > 1).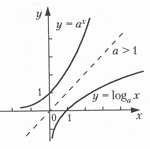



Рис. 2.18

Сложная функция.Пусть функция у = f (u) есть функция от переменной и,определенной на множестве U с областью значений Y, а переменная и в свою очередь является функцией и =  (х) от переменной х,определенной на множестве X с областью значений U. Тогда заданная на множестве X функция у = f [ (х)] называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функции). Например, у =lg sin x — сложная функция, так как ее можно представить в виде у = lg и,где и = sin x.

Понятие элементарной функции.Из основных функций новые функции могут быть получены двумя способами при помощи: а) алгебраических действий; б) операций образования сложной функции.

Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

(Например, функция   — элементарная.)

Классификация функций.Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).

Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся:

· целая рациональная функция (многочлен или полином):

y = a₀xⁿ+ a₁x^n- 1 + …+ a_n- 1x + a_n;

· дробно-рациональная функция отношение двух многочленов;

· иррациональная функция (если в составе операций над аргументом имеется извлечение корня).

Всякая неалгебраическая функция называется трансцендентной.К числу трансцендентных функций относятся: показательная, логарифмическая, тригонометрические, обратные тригонометрические, гиперболические функции.

Примерами неэлементарных функций являются функции: у = [х](читается «у равно антье х») — целая часть х (рис. 2. 19); у = sign x (читается «у равно сигнум х») — знак числа х. sign x = {-1, если х < 0; 0, если х = 0; 1, если х > 0} (рис. 2. 20); функция Дирихле.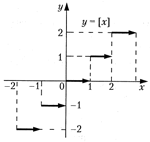



Рис. 2.19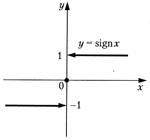



Рис. 2.20

Наиболее часто в экономике используются следующие функции.

1. Функция полезности (функция предпочтений)— в широком смысле зависимость полезности, т. е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия.

2. Производственная функция — зависимость результата производственной деятельности от обусловивших его факторов.

3. Функция выпуска (частный вид производственной функции) — зависимость объема производства от наличия или потребления ресурсов.

4. Функция издержек (частный вид производственной функции) — зависимость издержек производства от объема выпуска продукции.

5. Функции спроса, потребления, предложения — зависимость объема спроса, потребления, предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т. п.).

Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 45–54.

ФУНКЦИЯ
Понятие функции
	y = f (x) — функция f — правило (закон), по которому каждому элементу x ∈X ставится в соответствие одно определенное значение y ∈Y.
X — область определения функции, D (y) (множество значений x, для которых существует y).
Y — область значения функции, E (y) (множество значений y).
	x =  (y) — обратная функция, y = f–1 (x). Правило нахождения f–1 (x): 1. Из уравнения y = f (x) выразить x через y. 2. В полученном выражении поменять обозначения x на y, а y на x.
F (x ; y) = 0 — неявная функция (y не выражен через x).
y = f ( (x)) — сложная функция или функция от функции
Область определения некоторых функций
Вид функции			Область определения функции
			f(x) ≠ 0
			f(x) ≥ 0
3. loga f (x)			f(x) > 0
4.			–1 ≤ f(x) ≤ 1

Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 35.

5. 1. Найти область определения функции

Решение. Так как выражение под корнем четной степени должно быть неотрицательно, знаменатель дроби отличен от нуля, а выражение, стоящее под знаком логарифма, должно быть положительно, то область определения функции найдем из системы неравенства: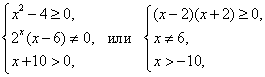



откуда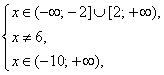 

Значения переменной x, которые удовлетворяют всем неравенствам системы одновременно, есть x ∈(–10; –2]   [2; 6)  (6; + ).

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 146.