ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 32 из 32

= 1 + 0,083333 + 0,0125 + 0,002232 + 0,000434 + 0,000089 +

+ 0,000018 +...   1,098606   1,0986.

(суммируем семь членов ряда — обоснование аналогично п. б).

г) Представим   в виде 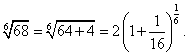  Так как после проведенного преобразования   входит в область сходимости (–1; 1) биноминального ряда, то при   получим, учитывая: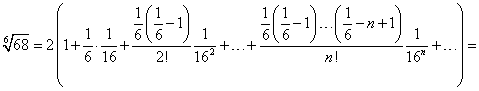



= 2 + 0,020833 – 0,000543 + 0,000021 – ….

(Для обеспечения данной в условии точности расчета достаточно взять три члена, так как по следствию из признака Лейбница для сходящегося знакочередующегося ряда погрешность |r_n| ≤ 0,000021 < 0,0001). Итак, 

д) Для вычисления   запишем при   принадлежащем области сходимости (– ; + ):



= 1 – 0,015231 + 0,000039 + …

(необходимо взять два члена, так как при этом погрешность

|r_n| ≤ 0,000039 < 0,0001).

Итак cos     1 – 0,015231 = 0,984769   0,9848.

е) «Точное» интегрирование здесь невозможно, так как интеграл «неберущийся». Заменив (–x2) в разложении, получим



Почленно интегрируя ряд на отрезке   принадлежащем интервалу сходимости (– ; + ), получим



+ … = 0,25 – 0,005208 + 0,000098 – …   0,24489   0,2449

(оценка погрешности производится также, как в примерах а) г) и д).

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 374–378,379–383.