ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 26 из 32

РЯДЫ

Тема 1. Числовые ряды

1.1. Числовые ряды

Пусть дана последовательность действительных положительных чисел



Определение 7.1. Выражение вида



называется числовым рядом с положительными членами.

a₁ — 1-й член ряда,

a₂ — 2-й член ряда,

…

a_n— n -й член ряда, и т. д.

Определение 7.2. Сумма первых k членов числового ряда называется k -й частичной суммой ряда и обозначается S_k.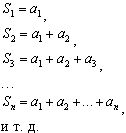



Определение 7.3.Если существует конечный предел частичных сумм   то числов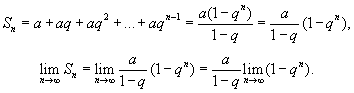ой ряд называется сходящимся и его сумма равна значению этого предела, иначе ряд называется расходящимся.

Пример 7.1.   — сумма бесконечной геометрической прогрессии.



При q < 1 ряд сходится и его сумма равна a /(1 - q).

При q > 1 ряд расходится.

Пример 7.2. 

Очевидно, что этот ряд расходится.

1.2. Свойства числовых рядов

Теорема 7.1.Если ряд   сходится и с — некоторое число, то сходится и ряд, причем выполняется равенство



Доказательство. Пусть S_n— частичная сумма исходного ряда. Так как ряд 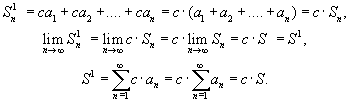  сходится, то 



Теорема 7.2.Пусть ряды   сходятся, тогда сходится ряд   причем 

Теорема 7.3.Сходимость ряда не изменится, если у него отбросить конечное число членов.

1.3. Необходимый признак сходимости ряда

Теорема 7.4(необходимый признак сходимости ряда). Если ряд сходится, то его n -й член стремится к нулю при n    .

Доказательство. Пусть ряд   сходится. Докажем, что 



Вычтем эти равенства:



Так как ряд сходится, то 



Полученный признак не является достаточным, т. е. из того, что   не следует, что ряд сходится. Этот признак поможет установить расходимость ряда: если признак не выполняется, то ряд расходится.

Пример 7.3.   — гармонический ряд.

 но ряд расходится.

1.4. Достаточные признаки сходимости числовых рядов с положительными членами

Теорема 7.5.(признак сравнения). Если члены двух числовых рядов   удовлетворяют неравенству a_n   b_nдля любых n, то из сходимости второго ряда следует сходимость первого ряда. Из расходимости первого ряда следует расходимость второго ряда.

Пример 7.4. Рассмотрим ряд   Сравним его с гармоническим рядом 



По признаку сравнения данный ряд расходится.

Теорема 7.6.(признак Даламбера). Если для числового ряда   существует конечный пр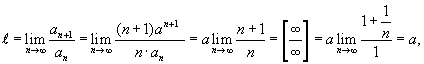едел отношения последующего члена ряда к предыдущему



а) при   < 1 ряд сходится;

б) при   > 1 ряд расходится;

в) при   = 1 вопрос о сходимости открыт.

Пример 7.5.  , a > 0.



при a< 1 ряд сходится, a> 1 ряд расходится.

Пример 7.6. 



Ряд расходится.

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 106–110.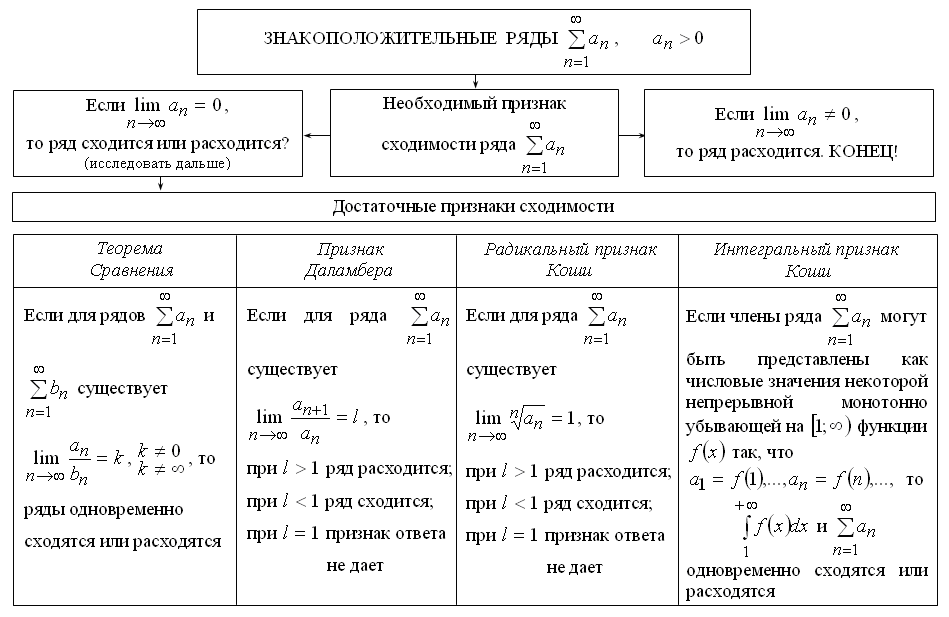





Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 72, 73.

13.14. С помощью признаков сравнения исследуйте данные ряды на сходимость:



Решение

а) Несколько членов данного ряда не являются положительными. Если отбросить конечное число членов этого ряда, он станет знакоположительным. Отбрасывание конечного числа членов ряда не влияет на сходимость или расходимость ряда, поэтому к этому ряду можно применить предельный признак сравнения. Если общий член ряда представляет собой отношение двух многочленов, то при подборе эталонного обобщенного гармонического ряда значение   выбирают равным разности наибольших показателей степеней знаменателя и числителя. Наибольший показатель степени знаменателя равен 3, числителя — 1, поэтому   = 3 – 1 = 2, и в качестве эталонного ряда возьмем обобщенный гармонический ряд с членами v_n = 1/ n2.

По формуле: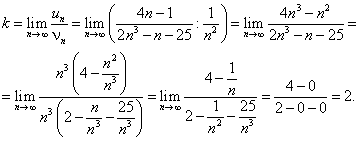



Поскольку предел к конечен и отличен от нуля, условие выполнено. На основании предельного признака сравнения заключаем, что исследуемый ряд, и эталонный ряд   ведут себя одинаково. Эталонный ряд сходится (обобщенный гармонический ряд,   = 2,), поэтому исследуемый ряд тоже сходится.

Замечание 1. Вычисление предела k необходимо для проверки правильности подбора эталонного ряда. Если получим, что k = 0 или k =  , то для применения предельного признака сравнения следует взять другой эталонный ряд.

б) Применим предельный признак сравнения. Подберем подходящий эталонный ряд. Рассмотрим поведение числителя и знаменателя общего члена ряда при больших п:





Поскольку при больших п величина   много больше, чем n, а величина n4 много больше, чем, то числителю условно припишем показатель степени 7/2, а знаменателю — 4. Возьмем   = 4 – 7/2 = 1/2, и в качестве эталонного ряда рассмотрим обобщенный гармонический ряд с членами v_n = 1/ n1,2. Найдем



Предел k конечен и отличен от нуля, условие предельного признака сравнения выполнено. Эталонный ряд расходится (обобщенный гармонический ряд,   = 1/2), поэтому исследуемый ряд тоже расходится.

в) Попытки применить предельный признак сравнения с эталонным рядом вида   не приводят к успеху: при разных   предел k равен или нулю, или бесконечности. Применим первый признак сравнения. Подберем эталонный ряд. При увеличении n функция п3растет гораздо быстрее, чем функция ln(n + 2), поэтому возьмем 

При n ≥ 1 выполняется цепочка неравенств:

ln(n + 2) ≥ 1, n3ln(n + 2) ≥ n3,

т.е. u_n≤ v_n.

Эталонный ряд   является обобщенным гармоническим рядом, у которого   = 3/2 > 1, поэтому он сходится. Члены исследуемого ряда не превосходят членов сходящегося ряда, значит, исследуемый ряд сходится.

г) Как и в пункте в), попытки применить предельный признак сравнения с эталонным рядом вида   не приводят к успеху: при разных   предел k равен или нулю, или бесконечности. Применим признак сравнения. Подберем эталонный ряд.

При увеличении n при всех   > 0 функция п αрастет гораздо быстрее, чем функция ln(n + 2). Возьмем   При достаточно больших п выполняется неравенство   откуда   т.е. u_n> v_n.

Эталонный ряд   является обобщенным гармоническим рядом, α = 3/4 < 1, поэтому он расходится. Члены исследуемого ряда больше членов расходящегося ряда, значит, исследуемый ряд расходится.

Замечание 2. В примере г) при подборе эталонного ряда нельзя просто отбросить ln(n + 2). Если взять   то, как и в примере в), можно показать, что u_n ≤ v_n. Однако ряд   pacxoдится (α = 1/4 < 1), и члены исследуемого ряда не больше членов расходящегося ряда, а в этом случае предельный признак сравнения не дает ответа на вопрос о сходимости или расходимости ряда 

д) Применим предельный признак сходимости. При n 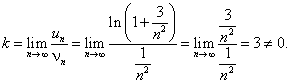   бесконечно малая величина ln (1 + 3/n2) эквивалентна 3/n2, и в качестве эталонного ряда возьмем ряд с членами v_n= 1/n2. По формуле найдем



Эталонный ряд сходится, и с ним вместе сходится исследуемый ряд.

е) Решение аналогично п. д). При n     бесконечно малая вели­чина sin ( /(2n + 1)) эквивалентна  /(2n + 1), и в качестве эталонного ряда возьмем ряд с членами v_n= 1/2n. По формуле найдем k = π   0. Эталонный ряд сходится, и с ним вместе сходится исследуемый ряд.

Замечание 3. В примерах а) – д) признак Даламбера не дает ответа на вопрос о сходимости рядов — во всех этих случаях   В примере e) l = 1/2, применение признака Даламбера возможно.

13.15. Исследовать сходимость рядов с помощью признака Даламбера:



Решение

а) Для того чтобы вычислить   преобразуем и_п+1/и_п:



Далее,



Поскольку l = 1/3 < 1, то по признаку Даламбера исследуемый ряд сходится.

б) Имеем  . Напомним, что по определению факториала n!= 1   2   3   ...   (n – 1)   n . Найдем l по формуле:



Поскольку l =  , то по признаку Даламбера исследуемый ряд расходится.

в) Имеем   Вычислим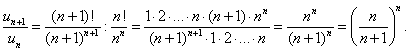



По формуле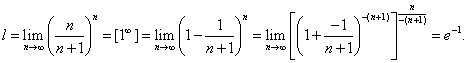



При вычислении предела мы воспользовались вторым замечательным пределом. Поскольку l = 1/е < 1, то по признаку Даламбера исследуемый ряд сходится.

г)По условию  . Используя определение факториала, получим что 

Найдем l по формуле: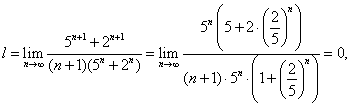



так как 5n сокращается,   а величина (n + 1)     при n    . Поскольку l = 0 < 1, то по признаку Даламбера исследуемый ряд сходится.

13.16. Исследовать сходимость ряда 

Решение

Применим интегральный признак сходимости. Рассмотрим 

Эта функция удовлетворяет всем условиям интегрального признака. По определению несобственного интеграла



Найдем



(при вычислении определенного интеграла мы воспользовались тем,   и применили формулу Ньютона–Лейбница

Далее,



Поскольку предел конечен, несобственный интеграл сходится, и по интегральному признаку сходимости исследуемый ряд тоже сходится.

Замечание. При попытке использовать признак Даламбера для исследования сходимости данного ряда получим, что l = 1, т.е. необходимо дополнительное исследование. При попытке найти эталонный ряд вида   и применить предельный признак сравнения получим, что k = 0 при   ≤ 1 или k =   при   > 1, т.е. применение предельного признака сравнения с эталонным обобщенным гармоническим рядом невозможно. Также невозможно исследовать сходимость этого ряда с помощью эталонных рядов вида   признака сравнения, поскольку члены исследуемого ряда при   ≤ 1 меньше членов расходящихся рядов, а при   > 1 они больше членов сходящихся рядов. В этих ситуациях признак сравнения не дает ответа на вопрос о сходимости ряда.

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 350–355.