ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 2 из 32

Тема 2. Понятие функции нескольких переменных

Пусть даны множества D   Rⁿи I   R.

Определение 12.1. Если каждой точке   множестваDставится в соответствие единственное число у из I, то говорят, что задана функция nпеременных у = f(x_1, …, x_n). Множество Dназывается областью определения функции D(у)= D, множество Iназывается множеством значений функции I(у)= I.

Если зафиксировать любые n- 1 переменные, то функция многих переменных превращается в функцию одной переменной. x₂ = с₂, x₃ = с₃, …, х_n= c_n; y = f(x_1, c_2, …, c_n) - функция одной переменной х₁.

Пример 12.1.

 — функция двух переменных,

 - функция трех переменных.

Определение 12.2. Графиком функции двух переменных (рис. 12.1) z = f(x, y) называется множество точек (х, у, z) 3-мерного пространства, таких, что (х, у) ∈D(z) и z= f(x, y). Любую точку графика можно записать в виде (х, у, f(x, y)).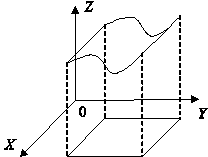



Рис. 12.1

Определение 12.3. Графиком функции nпеременных называется n-мерная гиперповерхность в пространстве R^n+ 1, точки которой имеют вид

(х₁, х₂, …, х_n, f(x₁, х₂, …, x_n)).

Определение 12.4. Линией уровня функции двух переменных называется линия на плоскости XOY, принадлежащая D(z), в каждой точке которой функция принимает одно и то же значение.

Уравнение линии уровня: f(x, y) = c, где с - произвольное число. На данной линии уровня значение функции z = c. Линий уровня бесконечно много, и через каждую точку области определения можно провести линию уровня.

Пример 12.2. z(x, y) =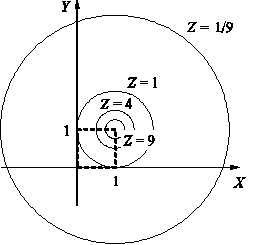 



D(z) = R² {(1,1)}.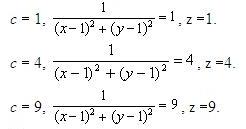



Используя линии уровня, можно построить график функции.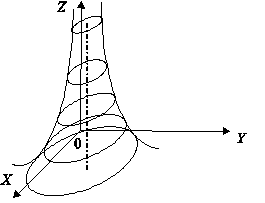



Определение 12.5. Поверхностью уровня функции nпеременных y = f(х₁, х₂, …, х_n) называется гиперповерхность в пространстве Rⁿ, входящая в D(у), в каждой точке которой значение функции одно и то же. Уравнение поверхности уровня f(х₁, х₂, …, х_n)= с. На поверхности уровня значение функции постоянно: у = с.

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 206–208.

15.1. Найти область определения функции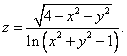 

Решение

Область определения представляет собой решение системы неравенств: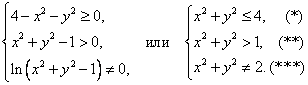



Множество значений х, у, удовлетворяющих (*), представляет собой внутренность круга с центром (0; 0) и радиусом, равным 2. Решения (**) — внешность круга радиуса 1 с центром (0; 0). Условие (***) означает, что в область определения не входит окружность с центром в начале координат и радиусом, равным   Таким образом, область определения представляет собой два кольца (см. рис. 15.1).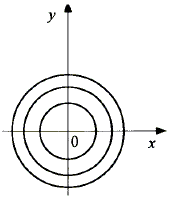



Рис. 15.1

15.2. Построить графики функций:

 б) z = 9 – x² – y².

Решение

a) Так как z > 0, график расположен выше плоскости Оху.Его чения плоскостями х = 0 и у = 0 представляют собой полуокружности радиуса 3 с центром в начале координат. «Нижняя» граница графика (пересечение с плоскостью Оху) представляет собой окружность радиуса3 (рис. 15.2).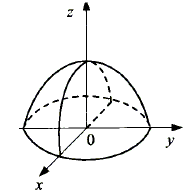



Рис. 15.2

б) В этом случае сечения графика плоскостями х = 0 и у = 0 представляют собой параболы с вершиной в точке (0; 0; 9) и ветвями, направленными вниз. Сечение плоскостью z = 0 есть окружность с центром в начале координат и радиуса 3. Функция не ограничена снизу. Ее график представлен на рис. 15.3.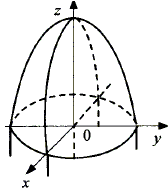



Рис. 15.3

15.3. Построить линии уровня функции 

Решение

Линии уровня имеют вид   т.е. представляют собой график функции   (x > 0, x ≠ 1). Функция определена при х > 0, имеет правостороннюю асимптоту, ось абсцисс, вертикальную асимптоту — ось ординат. Единственная критическая точка х = е — это точка максимума. Значение функции при этом   Таким образом, линии уровня имеют вид, показанный на рис. 15.4.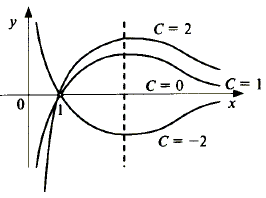

Рис. 15.4

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 390–391.

Если говорить точнее,то строго монотонными; к монотонным функциям, наряду с возрастающими и убывающими, относятся неубывающие и невозрастающие функции, т. е. такие, для которых при x₁,x₂ ∈X, удовлетворяющих условию х₂ > х₁,соответственно f(x₂) ≥ f(x₁) или f(x₂) ≤ f(x₁).

Под термином «период» подразумевается наименьший положительный период функции, равный 2 ; любой период функции у =sin x,как известно, равен 2  п,где п ∈Z.