ФУНКЦИИ. Тема Функции
 Скачать 1.59 Mb.
|
Тема 3. Вычисление пределов по правилу ЛопиталяТеорема 3.5. (Правило Лопиталя). Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует, т.е.  Пример 1. Пользуясь правилом Лопиталя, вычислить следующие пределы:  Решение 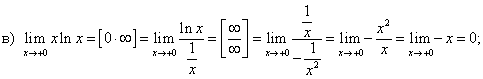   прологарифмируем обе части этого равенства. 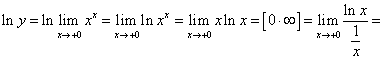 ln y = 0  y = e0 = 1. Таким образом, Замечание. Если после применения правила Лопиталя, отношение производных снова представляет собой неопределенность или и f'(x) и g'(x) удовлетворяют тем же требованиям, что и функции f(x) и g(x) и, то правило Лопиталя применяют повторно. Вывод о возможных случаях использования правила Лопиталя удобно представить в виде таблицы 3.1. Таблица 3.1
Цит. по: Математика для средних специальностей / Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 67–70. Тема 4. Дифференцируемость функции нескольких переменных4.1. Частные производные функции многих переменных Рассмотрим функцию двух переменных n = 2; z = f(x, y). Определение 11.8. Частной производной функции z = f(x, y) в точке (x0, y0) ∈ D(у) по соответствующей переменной называется предел отношения частного приращения функции по этой переменной к приращению этой переменной, когда приращение переменной стремится к нулю (если этот предел существует и конечен). 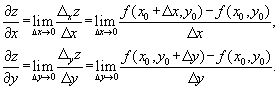 При введении частной производной по любой переменной остальные переменные были фиксированы. Данное определение совпадает с определением производной функции одной переменной. Следовательно, частную производную можно найти, зафиксировав все переменные, кроме одной, считая их постоянными. Производная находится как производная функции одной переменной, т. е.  Все правила и формулы, справедливые для производной функции одной переменной, остаются справедливыми и для частных производных. Пример 12.3. 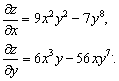 Пример 12.4.  4.2. Полный дифференциал Определение 12.7. Полным дифференциалом функции многих переменных называется главная линейная относительно приращений аргументов часть малого полного приращения функции. Рассмотрим функцию двух переменных n = 2; z = f(x, y). Если приращение функции  можно представить в виде где  ,  бесконечно малые функции при x 0, y 0, соответственно, то выражение dz =A x + B y называется полным дифференциалом функции двух переменных.Теорема 12.1.Полный дифференциал равен сумме попарных произведений частных производных на дифференциалы соответствующих переменных.  Пример 12.5. .  Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 209–210. 15.27. Найти частные производные функции Решение При дифференцировании по х считаем постоянной величину у. Таким образом, При дифференцировании по у считаем постоянной величину х, следовательно, Цит. по: Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. — 2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. — (Серия «Золотой фонд российских учебников») — С. 394. 4.3. Частные производные высших порядков Рассмотрим функцию двух переменных n = 2, z = f(x, y). Предположим, что функция имеет частные производные  которые являются функциями двух переменных. Их называют частными производными первого порядка. Предположим, что они дифференцируемы. Определение 12.11. Частные производные от частных производных первого порядка называются частными производными второго порядка.   — смешанные производные.Если полученные функции являются дифференцируемыми, то частные производные от них называются частными производными третьего порядка. Например:  Определение 12.12. Частной производной n -го порядка называется частная производная от частной производной (n - 1)-го порядка. Функция двух переменных имеет 2nпроизводных n -го порядка. Частная производная порядка р функции y = f(x1, x2, … xn) имеет вид  Теорема 12.5.Если частные производные первого порядка некоторой функции непрерывно дифференцируемы, то результаты смешанного дифференцирования равны.  Пример 12.6. z(x, y) = 5х3у - 4х2у5. 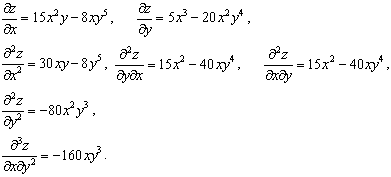 Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 215–216. 15.28. Найти частные производные второго порядка функции двух переменных z = ln(1 + x + 2у). Решение Частные производные 1-го порядка имеют вид: Считая их новыми функциями двух переменных, найдем их частные производные. Получаем:  Цит. по: Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. — 2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. — (Серия «Золотой фонд российских учебников») — С. 394. |