ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 10 из 32

Тема 2. Экстремум функции

Определение. Число f(x₀) называется наибольшим значением функции на отрезке [a, b], если для всех xиз этого отрезка выполняется неравенство f(x) ≤ f(x₀); число называется наименьшим значением функции на отрезке (a, b), если для всех xиз этого отрезка выполняется неравенство f(x) ≥ f(x₀).

Функция принимает свое наибольшее или наименьшее значение в точках экстремума или на границе. Для нахождения наибольшего и наименьшего значений функции на отрезке руководствуются следующим правилом: находят все критические точки функции (производная равна нулю), лежащие внутри отрезка, и находят значения функции в этих точках и на концах отрезка. Наибольшее из этих значений будет наибольшим, а наименьшее из этих значений — наименьшим значением функции на отрезке.

Пример. Найти наименьшее и наибольшее значение функции: f(x) = 2x³ – 9x² + 12x– 5 на отрезке [0; 3].

Решение. Находим f′(x) = 6x² – 18x+ 12 = 0 и приравниваем к нулю: 6x² – 18x+ 12 = 0 или x² – 3x+ 2 = 0.

Решая уравнение, находим критические точки x₁ = 1; x₂ = 2, причем обе лежат внутри отрезка.

Находим значение функции f(0) = – 5; f(1) = 0; f(2) = – 1; f(3) = 4. Наибольшее значение равно 4, а наименьшее – 5.

Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. —
Режим доступа к курсу: http://e-college.ru. —П. 8.4.

2. Точка х₀ называется точкой максимума (минимума) функции y = f(x), если существует интервал, содержащий точку х₀, такой, что для всех х из этого интервала имеет место неравенство f(x₀) ≥ f(x), f(x₀) ≤ f(x). Точки максимума и минимума называются точками экстремума.

3. Необходимое условие экстремума: в точке экстремума функции ее производная либо равна нулю (f'(x) = 0), либо не существует.

4. Первое достаточное условие экстремума: если в точке х₀ функция y = f(x) непрерывна, а производная f'(x) при переходе через точку х₀ меняет знак, то точка х₀ — точка экстремума: максимума, если знак меняется с «+» на «–», и минимума, если с «-» на «+».

Если при переходе через точку х₀ производная не меняет знак, то в точке х₀ экстремума нет.

5. Второе достаточное условие экстремума: если в точке х₀ f'(x₀) = 0, a f"(x₀) > 0, то х₀ является точкой максимума функции. Если f'(x₀) = 0, a f"(x₀) < 0, то х₀ является точкой минимума функции.

6. Схема исследования функции y = f(x) на экстремум:

1) найти производную y' = f'(x);

2) найти критические точки функции, в которых производная равна нулю или не существует;

3) исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции;

4) найти экстремальные значения функции.

При исследовании функции на экстремум с помощью 2-го достаточного условия п. 1), 2), 4) сохраняются, а в п. 3) необходимо найти вторую производную f"(x) и определить ее знак в каждой критической точке.

7. Чтобы найти наибольшее и наименьшее значение (глобальный максимум и минимум) функции y = f(x) на отрезке [a, b] следует выбрать наибольшее (наименьшее) из значений функции в критических точках, находящихся в интервале (a, b) и на концах отрезка (в точках а и b).

8. Если дифференцируемая на интервале (a, b) функция y = f(x) имеет единственную точку экстремума, то в этой точке достигается наибольшее или наименьшее значение (глобальный максимум или минимум) функции на интервале (a, b).

8.35. Найти интервалы монотонности и экстремумы функции 

Решение

В соответствии со схемой исследования (п. 6) найдем у' = 2х² – 5х + 2. Очевидно, производная существует при всех значениях х. Приравнивая у' к нулю, получаем уравнение 2х – 5х + 2 = 0, откуда   и x₂ = 2 — критические точки. Знаки производной имеют вид (рис. 8.1):



Рис. 8.1

На интервалах   и (2; + ) производная f′(x) > 0 и функция возрастает, на интервале   f′(x) < 0 и функция убывает;   — точка максимума и   x = 2 — точка минимума и   так как при переходе через эти точки производная меняет свой знак соответственно с «+» на «–» и с «–» на «+».

Замечание.

Установить существование экстремума в критических точках   и x = 2, в которых f′(x) = 0 можно было и с помощью второй производной f"(x) = 4 x – 5 (см. п. 5). Так как   а f"(2) = 3 > 0, то   — точка максимума, а х = 2 — точка минимума.

График данной функции схематично показан на рис. 8.2.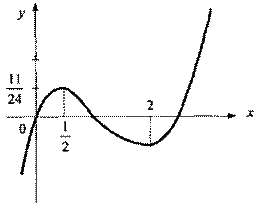



Рис. 8.2

8.36. Найти экстремумы и интервалы монотонности функции y = (x lnx – x)².

Решение



Производная существует во всех точках, в которых существует и сама функция, т.е. при х > 0. Точки, в которых производная обращается в нуль, задаются равенствами lnх = 0, lnx – 1 = 0, откуда x₁ = 1, x₂ = e — критические точки. Знаки производной указаны на рис. 8.3.



Рис. 8.3

Таким образом, функция монотонно возрастает на промежутках (0; 1) и (е; + ) и монотонно убывает на промежутке (1; e). Точка х = 1 — точка максимума и f_max(1) = 1, точка х = e — точка минимума и f_min(е) = 0.

8.37. Найти экстремумы и интервалы монотонности функции 

Решение

 Производная не существует при cosx = 1, т.е. при x = 2 n и равна нулю при x = π + 2 n. Знак производной совпадает со знаком sinx; таким образом у' > 0 при 2 k < х < π + 2 k и у' < 0 при –π + 2 k < x < 2 k. Это, соответственно, интервалы возрастания и убывания функции. x = π + 2 k — точки максимума   x = 2 k — точки минимума f _min (2 k) = 0.

8.39. Найти наибольшее значение (глобальный максимум) функции   на интервале (10; 18).

Решение

Найдем 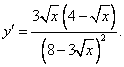  На интервале (10; 18) имеется всего одна критическая точка х = 16. Производная при переходе через эту точку меняет знак с «+» на «–», т.е. х = 16 — точка максимума. Следовательно, функция достигает наибольшего значения при х = 16, т.е. f_наиб = f_max(16) = –16. (Заметим, что наименьшего значения (глобального минимума) данной функции на указанном интервале не существует.)

8.40. Забором длиной 24 м требуется огородить с трех сторон прямоугольный палисадник наибольшей площади. Найти размеры палисадника.

Решение

Пусть длины сторон палисадника х, у. Тогда 2х + у = 24, т.е. у = 24 – 2х. Площадь палисадника S = xy = x(24 – 2x) = 24x – 2x^2, где 0 < x < 12 (ибо 24 – 2x > 0). Таким образом, задача свелась к отысканию значения х, при котором S(x) принимает наибольшее значение на интервале (0; 12). Найдем S'(x) = 24 – 4х = 0 при х = 6. Легко видеть, что х = 6 — единственная точка экстремума — максимума функции S(x). Это означает, что на интервале (0; 12) S(x) принимает наибольшее значение при х = 6, т.е. искомые размеры палисадника 6 м и 24 – 2 * 6 = 12 м.

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 216–220.