ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 18 из 32

Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 58–59.

11.30. Найти площади плоских фигур, ограниченных линиями:

а) у = х²;   x = 3, у = 0;

б) у = 2х – х², у = 0, х = 3;

в)   у = 4х,   (фигура расположена в первой четверти);

г) у = ln х, у = ln (х + 1), у = 1, у = – 1.

Решение:

а) Искомая площадь S = S_OAB — это площадь под «кривой» ОАВ (см рис. 11.6) на отрезке [0; 3].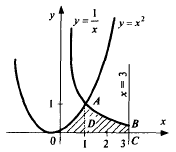



Рис. 11.6

Линия ОАВ состоит из части ОА параболы у = х² и части АВ гиперболы у = 1/x. Соответственно, площадь S найдем как сумму двух площадей: S = S_OAD + S_ABCD, каждую из которых вычислим, опираясь на геометрический смысл определенного интеграла. Решая систему

находим координаты точки А: (1, 1).

Тогда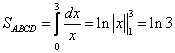







б) Фигура искомой площади S состоит из двух криволинейных треугольников: ОАВ и BCD, расположенных (соответственно) выше и ниже оси Ох (см. рис. 11.7). Площади этих треугольников найдем по формулам <…> и <…> :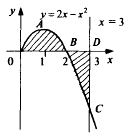



Рис. 11.7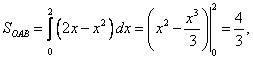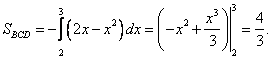





Тогда 

в) Найдем координаты точек пересечения заданных линий (см. рис. 11.8).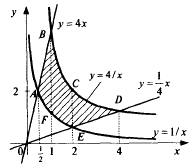



Рис. 11.8

Решая систему   получаем А(1/2; 2). Аналогично B(1; 4), D(4; 1), E(2; 1/2).

Искомой в данном случае является площадь S криволинейной трапеции ABDE. Выполняя проецирование «угловых» точек этой трапеции на ось Ох, разобьем ее на части, площадь каждой из которых найдем по формуле :

S = S_ABF + S_BCEF + S_CDE;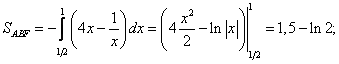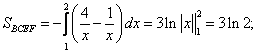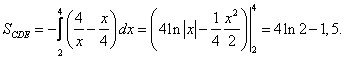







Окончательно получаем:

S = (l,5 – ln 2) + 31n 2 + (4ln 2 – 1,5) = 6ln 2   4,2(ед2).

г) Искомой здесь (см. рис. 11.9) является площадь криволинейной трапеции ABCD. В данном случае будет удобно использовать проецирование фигуры на ось Оу, т.е. поменять местами функцию у и аргумент х.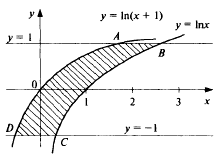



Рис. 11.9

Используя формулу (с учетом последнего замечания), получаем: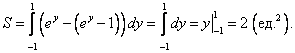



Заметим, что использование традиционного проецирования фигуры на ось Ох приведет к существенно более трудоемкому решению (предлагаем читателю в качестве упражнения убедиться в этом самостоятельно).

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 295–297.