ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 15 из 32

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Тема 1. Площадь криволинейной трапеции и определенный интеграл

1.1. Определенный интеграл и его свойства

К понятию определенного интеграла приводят самые разнообразные задачи: определение площади плоской фигуры; нахождение работы переменной силы, нахождение по заданной переменной скорости и многие другие. Рассмотрим некоторые из них.

Задача о работе переменной силы. Пусть требуется найти работу по перемещению материальной точки, движущейся из точки В (b) в точку С (с) вдоль оси Ох под действием переменной силы F = f (x) (рис. 5.1).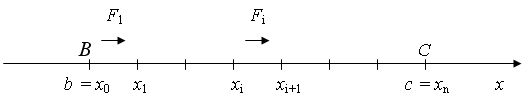



Рис. 5.1

Из курса физики известно, что работа по перемещению материальной точки под действием постоянной силы F равна скалярному произведению вектора силы на вектор перемещения, т.е.

Решение этой задачи основано именно на этом факте.

Для нахождения работы по перемещению материальной точки под действием переменной силы разобьем отрезок [b,c] на n частичных отрезков точками:

b = x₀, x₁, …, x_i– 1, x_i, …, x_n= с

и положим  .

Наибольшую из этих разностей обозначим λ, т.е.

Внутри [x_i– 1, x_i] возьмем точку   и предположим, что на этом отрезке действует постоянная сила F_i, равная силе, приложенной в точке  _, т.е. F_i= f ( ). Тогда работа на участке x_i будет определятся так:

A_i= f (x _i)   x_i

Так как работа на всем пути ВС равна сумме работ, соответствующих отдельным участкам разбиения пути ВС, то

 (5.1)

Задача о площади криволинейной трапеции. Пусть требуется найти площадь плоской фигуры аАВb (рис. 5.2), ограниченной графиком функции y = f (x), непрерывной и неотрицательной на отрезке [a, b], и отрезками прямых у = 0, х = а, х = b. Такая фигура называется криволинейной трапецией.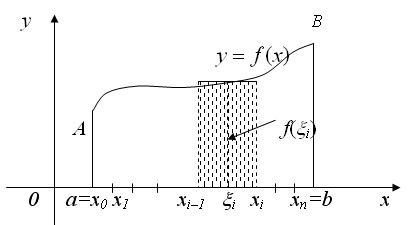



Рис. 5.2

Разобьем отрезок точками [a; b] точками

a = x₀ < x₁ < … < x_i– 1 < x_i< … < x_n= b

на n частичных отрезков и положим

.

Наибольшую из этих разностей обозначим λ, т.е.

На отрезке [x_i – 1 ; x_i] выберем точку  и найдем значение функции f (x) в точке  . На частичных отрезках построим как на основаниях прямоугольники с высотами равными f ( ). В итоге получится ступенчатая фигура, площадь которой будет приближенно равна площади данной криволинейной трапеции.

Площадь прямоугольника, соответствующего частичному отрезку  x_iравна

S_i= f (x_i)   x_i

Тогда площадь криволинейной трапеции будет приближенно равна площади ступенчатой фигуры, состоящей из прямоугольников, т.е.

 (5.2)

Аналогично решаются задачи о нахождении пути по известной скорости, массы плоской кривой, если известна ее плотность и многие другие.

И хотя все эти задачи различны по содержанию, последовательность и результат математических действий в ходе их решения одинаковы:

1. Отрезок [a, b], на котором задана непрерывная функция f (x), разбивается на n частичных отрезков.

a = x₀ < x₁ < … < x_i– 1 < x_i< … < x_n= b

2. Выбирается i участок  , 

3. Берется точка  ∈ [x_i–1 ; x_i], находится значение функции в этой точке, f ( ), и умножается на длину интервала  x_i, т.е.

f (x_i)   x_i

4. Составляется сумма этих произведений

 (5.3)

Сумма (5.3) называется интегральной суммой.

5. Находится предел суммы (5.3) при λ   0, т.е.

Этот предел и называется определенным интегралом от функции f(x) в пределах от а до b, обозначается  _.

Определение. Определенным интегралом от функции f (x) на [a; b] называется предел интегральной суммы вида   при λ   0, где   Если этот предел не зависит от способа разбиения отрезка [a; b] на части и выбора точки  _.

Записывается это так: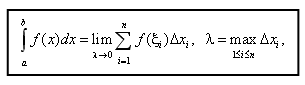

 (5.4)

где f (x) — подынтегральная функция;

f (x)dx — подынтегральное выражение;

а — верхний предел интегрирования;

b — нижний предел интегрирования.

Если определенный интеграл (5.4) существует, то функция f(x) называется интегрируемой на отрезке [a; b].

Справедлива следующая теорема.

Теорема 5.1 (достаточное условие существования определенного интеграла). Если функция y = f(x) непрерывна на отрезке [a; b], то она интегрируема на этом отрезке.

Цит. по: Математика для средних специальностей /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 111–115