ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 13 из 32

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Тема 1. Определение первообразной. Неопределенный интеграл

1.1. Первообразная. Неопределенный интеграл

Определение 5.1. Первообразной функцией F(x) для функции f(x) называется функция, производная которой равна исходной функции.

(F(x))' = f(x).

Теорема 5.1(теорема Коши). Любая непрерывная на некотором множестве функция имеет на этом множестве первообразную.

Пример 5.1. Функция F(x) = x³ является первообразной функции f(x) = 3x² так как (x³)' = 3x². Функции F₁(x) = x³ + 3 и F₂(x) = x³ - 2 также являются первообразными функции f(x). Любая функция вида F(x) = x³ + с, где с — произвольное число, является первообразной функции f(x).

Каждая функция может иметь бесконечно много первообразных, которые отличаются на постоянное слагаемое. Верно и обратное утверждение.

Теорема 5.2.Если F₁(x) и F₂(x) — две первообразные для функции f(x), то они отличаются на постоянное слагаемое.

Доказательство. Рассмотрим функцию

Ф(х)= F₁(x)- F₂(x).

Ф'(х)= F₁'(x)- F₂'(x)= f(x)- f(x)= 0,

Ф(х)= C,

F₁(x ) = F₂(x) + C.

Определение 5.2.Совокупность всех первообразных данной непрерывной функции называется неопределенным интегралом от этой функции и обозначается  , где f(x)именуется подынтегральной функцией, выражение f(x)dx — подынтегральным выражением.

Если F(x) — некоторая первообразная данной функции, то   = F(x)+ C, где C — произвольная постоянная.

Процесс нахождения неопределенного интеграла называется интегрированием данной функции, или взятием интеграла от данной функции.

Первообразные имеют следующий геометрический смысл.

Пусть F₁(x) и F₂(x) — первообразные функции y = f(x). Найдем их производные в точке х₀.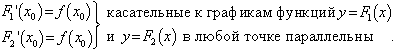



Следовательно, и сами графики будут располагаться параллельно (рис. 5.1).

На основании теоремы 5.2 F₁(x) и F₂(x) отличаются на постоянное слагаемое, следовательно, один график можно получить из другого сдвигом на C единиц вдоль оси ОY.

F₁(x) = F₂(x) + C.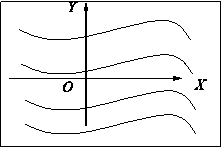



Рис. 5.1

Функция имеет бесконечно много первообразных, которые отличаются друг от друга на постоянное слагаемое. Графики всех первообразных представляют собой бесконечное семейство параллельных кривых.

1.2. Свойства неопределенного интеграла

Теорема 5.3.Производная от неопределенного интеграла равна подынтегральной функции, дифференциал от неопределенного интеграла равен подынтегральному выражению.

Доказательство. Пусть функция f(x) имеет первообразную F(x), тогда

 = F(x) + c.

Найдем производную и дифференциал от обеих частей равенства.

 = (F(x)+ c)' = f(x),

d ( ) = ( )' dx = f(x)dx.

Теорема 5.4. Интеграл от дифференциала функции равен этой функции с точностью до постоянного слагаемого.

Доказательство.   =  = f(x)+ C.

Из теорем 5.3 и 5.4 следует, что операции дифференцирования и интегрированияявляются взаимообратными.

Теорема 5.5.Постоянный множитель можно выносить за знак интеграла.

Доказательство. Пусть функция f(x) имеет первообразную F(x).

 = F(x) + C.

Умножим обе части на k.

k   = k F(x) + C₁, где C₁ = kC.

Найдем производную функции k F(x).

(k F(x))' = kf(x).

Функция k F(x) является первообразной функции k f(x). Следовательно,

 = k F(x) + C,

 = k  .

Теорема 5.6.Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.



1.3. Таблица основныхнеопределенных интегралов

Теорема 5.7.Пусть функция u =  (t) определена и дифференцируема на некотором промежутке Т, а Х — множество значений этой функции, на котором определена функция f(x). Функция у = f(x) имеет первообразную F(x)на множестве Х и

 = F(x)+ с.

Тогда

 = F(u)+ с.

Доказательство. Пусть u =  (x) — некоторая дифференцируемая функция.

(F(u))' = (F( (x)))' = f(φ(x))  '(x),

F(u) является первообразной для функции f( (x))  '(x).

f(u) du =  f( (x))d  (x)=  f(φ(x))  '(x)dx = F(u)+ с.

Из теоремы следует, что в любом табличном интеграле можно заменить аргумент дифференцируемой функцией.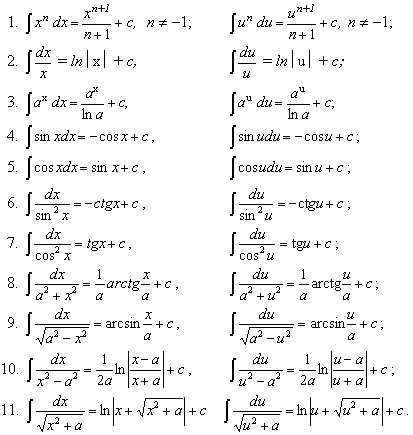



Эти формулы легко доказываются дифференцированием правой части.

1.4. Непосредственное интегрирование

Этот вид интегрирования состоит в приведении исходного интеграла к одному или к нескольким табличным с помощью свойств интеграла и тождественных преобразований.

Пример 5.2. 

Пример 5.3.


Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 64–68.

10.1. Найти неопределенные интегралы:

Решение: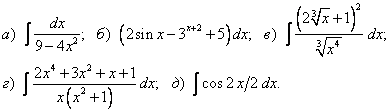



а) Вынося постоянный множитель   за знак интеграла, приходим к табличному интегралу при а = 3/2: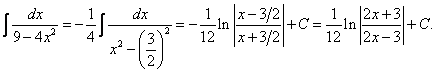



б) Используя свойства интеграла и, приходим к сумме табличных интегралов, при а = 3 и при п = 0: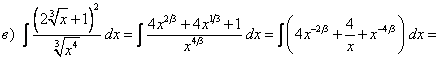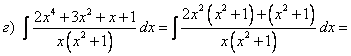











= x² + ln|x| + arctg x + C.



Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 264.