ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 12 из 32

Тема 4. Исследование функции

4.1. План исследования функции

Если требуется построить график функции y = f(x), то надо предварительно исследовать эту функцию. Для исследования рекомендуется следующий план:

1) найти область определения D(f);

2) найти точки разрыва, вертикальные асимптоты;

3) найти асимптоты;

4) найти точки пересечения графика с осями координат;

5) определить четность (f(–x) = f(x)) или нечетность (f(–x) = –f(x)), т.е. является ли график этой функции симметричным относительно оси ординат, или начала координат, или же такой симметрии нет;

6) найти экстремумы, интервалы возрастания и убывания;

7) найти точки перегиба, интервалы выпуклости и вогнутости. На основании этого исследования строится график функции.

Если в каких-то местах ход графика остается неясным, то находят дополнительные точки на этом графике.

Пример. Исследовать функцию   и построить ее график.

Решение. Исследуем функцию по рекомендованному плану.

1. D(f): (– ; –1)   (–1;  ).

2. Точка разрыва x = –1, вертикальная асимптота x = –1.

3. Найдем невертикальную асимптоту y = kx + b.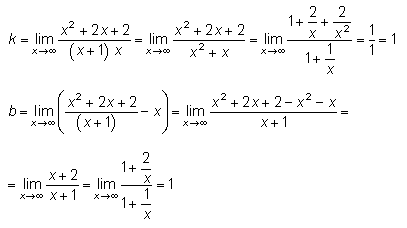



Итак, уравнение невертикальной асимптоты y = x + 1.

4. При x = 0 находим точку пересечения с осью ординат y = 2. При y = 0 получаем уравнение x² + 2x + 2 = 0. Это уравнение не имеет решений (D < 0), следовательно, график не имеет пересечения с осью абсцисс.

5. Проверим, является ли функция четной или нечетной.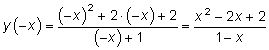





Функция не является ни четной, ни нечетной, поэтому у ее графика нет симметрии ни относительно оси ординат, ни относительно начала координат.

6. Найдем точки экстремума и интервалы возрастания и убывания функции.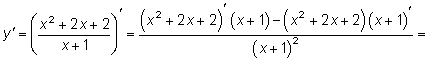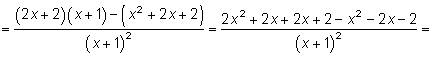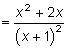







Найдем критические точки, приравняв производную нулю: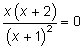



Критические точки x = 0 и x = –2. Эти точки разбивают область определения функции на четыре интервала. Рассмотрим результат исследования в таблице.

х	(– ; –2)	–2	(–2; –1)	(–1; 0)	0	(0; + )
y'	+	0	–	–	0	+
y	возрастает	max	убывает	убывает	min	возрастает

7. Определим интервалы выпуклости, вогнутости и точки перегиба.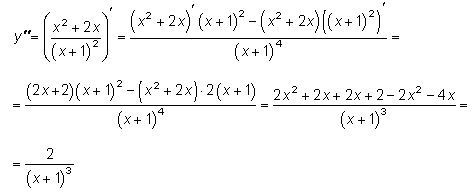



Итак, y'' не обращается в нуль ни в одной точке, следовательно, точек перегиба нет. Построим таблицу:

х	(– ; –1)	(–1; + )
y''	–	+
y

Занесем все данные в одну общую таблицу:

х	(– ; –2)	–2	(–2; –1)	(–1; 0)	0	(–1; +  )
y'	+	0	–	–	0	+
y''	–		–	+		+
y	возрастает	max –2	убывает	убывает	min 2	возрастает

Учитывая проведенное исследование, построим график: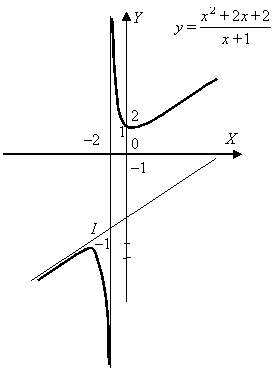



Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. —
Режим доступа к курсу: http://e-college.ru. —П. 8.4.

Пример 16

Исследовать функцию   на монотонность и экстремум.

План решения

1. Найти область определения функции, D(y).

2. Найти y'.

3. Найти значения х ∈ D(y), при которых y' = 0 или не существует. Нанести их на числовую прямую.

4. Определить знак y' слева и справа от найденных точек.

5. Сделать вывод:



Решение

1. D(y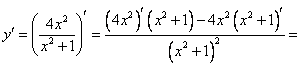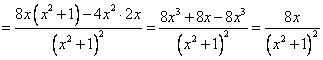): (– ; + ), т.к. знаменатель дроби никогда не обращается в нуль как сумма квадратов.

2. 

.

3.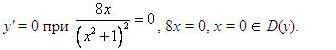 

4.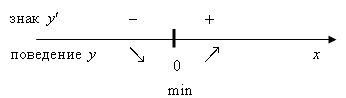



(– ; 0] — промежуток убывания,

[0; + ) — промежуток возрастания,

х = 0 — точка минимума.

Пример 18

Найти вертикальные асимптоты к графику функции 

План решения

x = a — вертикальная асимптота, если.

1. Найти область определения функции.

2. Найти точки разрыва функции.

3. Найти пределы функции слева и справа от точек разрыва. Если эти пределы равны ± , то прямые, проходящие через эти точки будут вертикальными асимптотами.

Решение

Так как x² + 2x ≠ 0, то x (x + 2) ≠ 0   x ≠ 0, x ≠ – 2.

Область определения: D(y) = (– ; – 2)   (– 2; 0)   (0;  ).

х= 0 и х = - 2 — точки разрыва.

Найдем односторонние пределы.

,

.

Следовательно х = - 2 — вертикальная асимптота.

,

.

Следовательно х = 0 — вертикальная асимптота.

Цит. по: Методическое пособие-тренажер решения задач по высшей математике /
Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 50–51.