ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 20 из 32

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Тема 1. Дифференциальные уравнения первого порядка

1.1. Понятие о дифференциальном уравнении

Определение 6.1.Уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков, называется дифференциальным уравнением.

Определение 6.2.Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.

Дифференциальное уравнение n -го порядка имеет вид

F(x, y, y', y'', …, y⁽ⁿ⁾) = 0.

Определение 6.3.Дифференциальное уравнение n -го порядка называется линейным, если неизвестная функция и все ее производные входят в него в первой степени. Общий вид линейного дифференциального уравнения n -го порядка:

a₀(x)y⁽ⁿ⁾ + a₁(x)y^{(n - 1)} +... + a_n - 1(x)y⁽¹⁾ + a_n(x)y = f(x). (6.1)

Определение 6.4.Линейное дифференциальное уравнение (6.1) называется однородным, если f(x)   0, и неоднородным — в противном случае.

Примеры дифференциальных уравнений:

y'' - sin x y' + (cos x) y = tg x — линейное,

sin y' - cos y = ctg x — нелинейное,

y'' ' - y' = 0— линейное,

(y^IV)² - 3y'' ' + y = 1 — нелинейное.

Определение 6.5.Решением дифференциального уравнения называется любая функция y = 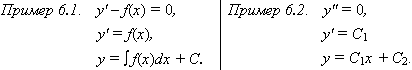 (x), при подстановке которой в уравнение будет получено тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения, график решения называют интегральной кривой.



Определение 6.6. Решение дифференциального уравнения n -го порядка, содержащее n произвольных постоянных, называется общим решением дифференциального уравнения.

Определение 6.7.Если в результате интегрирования дифференциального уравнения получена зависимость между y и x, из которой не удается явно выразить y через x (т. е. неизвестная функция задана неявно), то данную зависимость называют общим интегралом дифференциального уравнения.

Определение 6.8.Решение, полученное из общего при конкретных значениях произвольных постоянных, называется частным решением.

Пример 6.3.

y'' + y = 0.

y = C₁ cos x + C₂ sin x — общее решение.

у₁ = 3cos x - 2sin x — частное решение.

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 97–98.

Теорема о существовании и единственности решения. Рассмотрим геометрический смысл дифференциального уравнения первого порядка

y' = f(x, y), (6.53)

которое в каждой точке (x, y) плоскости Oxy сопоставляет направление tg a = f(x, y) касательной к интегральной кривой y = y(x), проходящей через эту точку. Говорят также, что уравнение (6.53) задает поле направлений в области Г (рис. 6.23).



Рис. 6.23

Решить уравнение (рис. 6.23) — значит найти семейство кривых, отвечающих заданному полю направлений.

Теорема. Пусть в дифференциальном уравнении (рис. 6.53) функция f(x, y) и ее частная производная   непрерывны на открытом* множестве Г координатной плоскости Oxy.

1. Для всякой точки (x₀, y₀) множества Г найдется решение y = y(x) уравнения (6.53), удовлетворяющее условию y₀ = y(x₀).

2. Если два решения y = y₁(x) и y = y₂(x) уравнения (6.53) совпадают хотя бы для одного значения x = x₀, т.е. если y₁(x₀) = y₂(x₀), то эти решения совпадают для всех тех значений переменной x, для которых они определены.

Геометрический смысл теоремы состоит в том, что через каждую точку (x₀, y₀) множества Г проходит одна и только одна интегральная кривая уравнения (6.53) (рис. 6.24).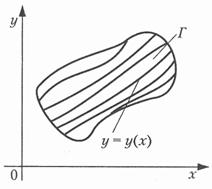



Рис. 6.24

Задача отыскания частного решения дифференциального уравнения (6.53), удовлетворяющего условию y(x₀) = y₀, называется задачей Коши. Приведенная теорема устанавливает условие существования и единственности решения задачи Коши.

Приведем пример уравнения, для которого не выполняется условие единственности решения, т.е. существует такая точка плоскости Oxy, через которую проходит более одной интегральной кривой. Пусть y' = y^2/3. Проверяем непосредственно, что y = 0 и   — решение данного уравнения, проходящие через точку (0; 0).

Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 234–235.

1.2. Дифференциальные уравнения с разделяющимися переменными

Дифференциальными уравнениями с разделяющимися переменными называют уравнения вида

X₁(x) Y₁(y)dx + X₂(x) Y₂(y)dy = 0.

Перенесем второе слагаемое в правую часть.

X₁(x) Y₁(y)dx = - X₂(x) Y₂(y)dy.

Предположим, что Y₁(y) X₂(x)   0. Разделим обе части уравнения на это произведение:



Переменные разделились. Интегрируя обе части этого равенства, получим общее решение уравнения:



Пример 6.4. 

dy = y' 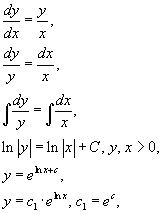dx, y' = 



y = c₁ x — общее решение уравнения.

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 98–99.

12.1. Доказать, что функция

у = С₁е^х + С₂е^2х (12.1)

является решением уравнения

у" – 3у' + 2у = 0. (12.2)

Решение. Последовательно дифференцируя (12.1), приходим к равенствам:

y' = С₁е^х + 2С₂е^2х,

у" = С₁е^х + 4С₂е^2х.

Решая эту систему относительно С₁е^х и С₂е^2х, получаем:

С₁е^х = 2y' – у",

Подставляя эти выражения в (12.1), приходим к (12.2).

12.2. Проверить, что функция

у³ – Сх³ + 3ху = 0 (12.3)

является интегралом уравнения

у³ – (ху² + х²)у' + 2ху = 0. (12.4)

Решение. Дифференцируя (12.3) по х в предположении, что у = у (х), приходим к равенству

у²у' – Сх² + у + ху' = 0,

откуда

Сх² = (у² + х )у' + у.

Подставляя выражение для Сх² из последнего равенства в (12.3), имеем:

у³ – (у²y' + хy' + y) x + 3ху = 0,

что равносильно (12.4).

12.3. Найти дифференциальное уравнение семейства кривых

y = C(x – C)². (12.5)

Решение. Дифференцируя (12.5) по переменной х, получаем

y' = 2C(x – C), (12.6)

откуда

С² = Сх – 5у'. (12.7)

С помощью равенства (12.7) преобразуем (12.5) так, что постоянная С будет входить в запись слагаемых полученного выражения в степенях не более первой:

у = 0,5 ху' – 0,5Су'.

Следовательно,

Су' = ху' – 2у. (12.8)

Умножая (12.6) на (у')², получаем

(у')³ = 2ху'(Су') – 2(Су')².

Исключая из полученного равенства Су' с помощью (12.8), окончательно имеем:

(у')³ =4хyу' – 8y^2.

12.4. Найти решение уравнения

удовлетворяющие начальному условию у(0) = 1.

Решение. Из определения неопределенного интеграла, следует, что общее решение заданного уравнения имеет вид:

Используя преобразование переменной под знаком дифференциала, получаем

Учитывая начальное условие, приходим к равенству 1 = 1 + С, откуда С = 0. Таким образом, искомое частное решение имеет вид:

Геометрически найденная функция представляет интегральную кривую дифференциального уравнения, проходящую через точку (0, 1).

12.15. Решить уравнение:

yx²dy – ln xdx = 0. (12.10)

Решение. Исходное уравнение перепишем в виде

_. (12.11)

Таким образом, имеем уравнение с разделяющимися переменными и из (12.11) следует:

Интеграл левой части — табличный. Для нахождения интеграла правой части воспользуемся формулой интегрирования по частям, где и = ln x,  :

Окончательно интеграл уравнения (12.10) имеет вид:

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 316–318, 319.

*На множестве, содержащем с каждой своей точкой некоторую окрестность этой точки.