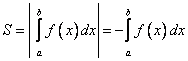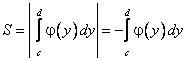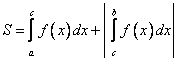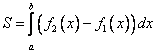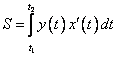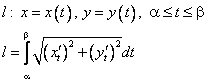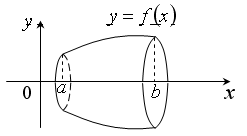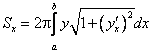ФУНКЦИИ. Тема Функции
 Скачать 1.59 Mb. Скачать 1.59 Mb.
|
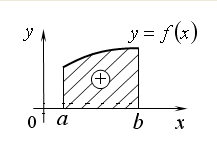
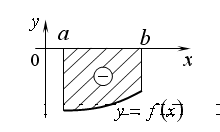
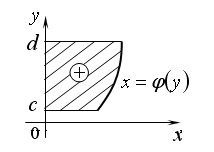
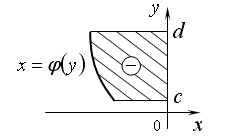
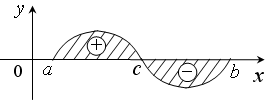
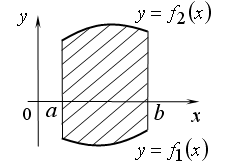
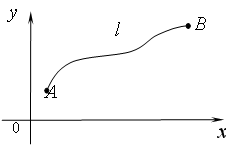
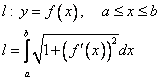
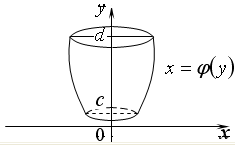
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛАТема 1. Вычисление площадей плоских фигур с помощью интеграла1.1. Приложения определенного интеграла Вычисление площадей фигур, расположенных под (над) графиком функции на некотором отрезкеЭто приложение вытекает из геометрического смысла определенного интеграла. 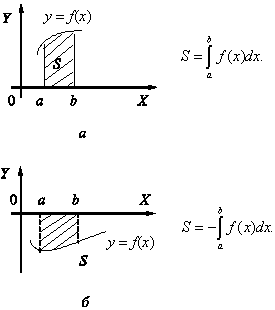 Рис. 5.5 Вычисление площади фигур, ограниченных графиками двух функций на некотором отрезке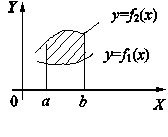 Рис. 5.6 S = S2 - S1 = где S1 и S2 — площади криволинейных трапеций под графиками функций y = f1(x)и y = f2(x). Пример 5.18. 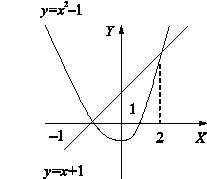 y = x2 - 1, y = x + 1. Найдем абсциссы точек пересечения. x2 - 1= x + 1, x2 - x - 2= 0, x1 = 2x2 = - 1. 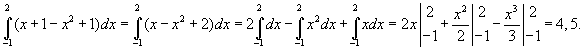 Вычисление объемов тел, полученных от вращения графика функции вокруг оси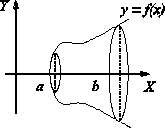 Рис. 5.7 Пример 5.19. y = sinx, x ∈ [0, 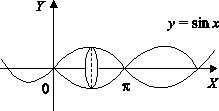 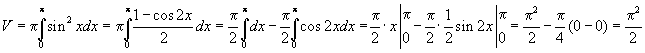 Вычисление объемов тел, полученных от вращения графика функции вокруг оси ОY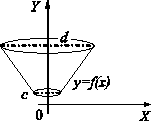 Рис. 5.8. где x = f-1(y) — обратная функция к функции y = f(x). Пример 5.20. y = , y ∈ [1,4]. 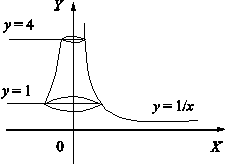 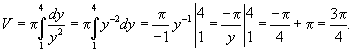 Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 83–86.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||