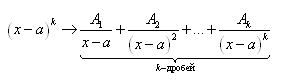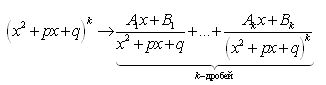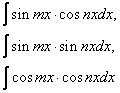ФУНКЦИИ. Тема Функции
 Скачать 1.59 Mb.
|
Тема 2. Методы интегрирования2.1. Основные методы интегрирования Метод замены переменнойВо многих случаях интеграл можно упростить и свести его к табличному, если ввести новую переменную интегрирования. Метод замены переменной (или метод подстановки) — один из основных методов интегрирования, он описывается следующей формулой:  где x =  (t) — функция дифференцируемая на некотором рассматриваемом промежутке.Докажем данную формулу. Формула (4.9) справедлива, если после дифференцирования обеих ее частей получатся одинаковые выражения. Учитывая, что f(x) = f( 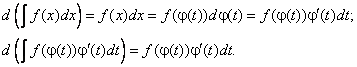(t)) — сложная функция, найдем дифференциалы обеих частей равенства (4.9). Таким образом, формула (4.9) верна. Следует заметить, что все способы интегрирования имеют целью свести данный интеграл к табличному с помощью тех или иных искусственных приемов. Интегрирование методом подстановки предполагает: 1. Определить, к какому табличному интегралу приводится данный (или от чего вы хотите избавиться под знаком интеграла). 2. Определить, какую часть подынтегральной функции заменить новой переменной и записать эту замену. 3. Продифференцировать подстановку. Сделать замену под интегралом. 4. Найти интеграл. 5. Вернуться к прежней переменной. Пример 2. Найти интегралы  Решение  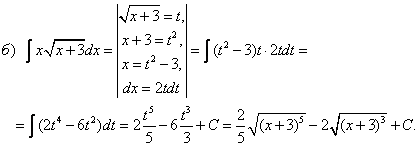 Метод «подведения» под знак дифференциалаОчень часто при вычислении интегралов пользуются приемом «подведения» подынтегральной функции под знак дифференциала («внесения» под знак дифференциала). По определению дифференциала имеем '(x)dx = d( (x))Переход от левой части этого равенства к правой называют подведением множителя '(x) под знак дифференциала.Пусть требуется найти интеграл 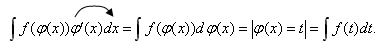 При интегрировании методом «подведения» под знак дифференциала следует помнить свойства дифференциала. Пример 2. Найти интегралы  Решение 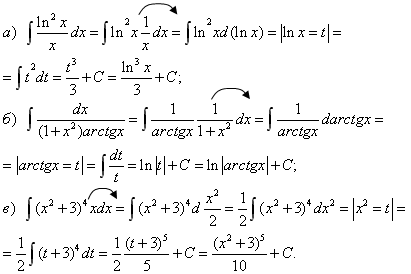 Замечание. Легко заметить, что если  Вывод: если под знаком интеграла в числителе дроби стоит дифференциал знаменателя, то интеграл равен логарифму знаменателя. Формулу (4.10) целесообразно внести в таблицу интегралов. 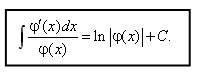 (4.10)Пример 3. Найти интегралы  Решение Для решения воспользуемся формулой (4.10).    Метод интегрирования по частямПусть u(x) и v(x) — непрерывно дифференцируемые функции. Как известно d(u  v) = vdu + udvИз этого равенства следует, что udv = d(u v) – vdu.Проинтегрировав последнее соотношение, получим 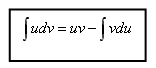 (4.11)(произвольная постоянная С включена в  ).Формула (4.11) и есть формула интегрирования по частям. Как правило, данный метод интегрирования используется в тех случаях, когда интеграл, стоящий в правой части формулы (4.11) проще данного или такой же. Возникает вопрос, что же в исходном интеграле принять за u и что за dv? Ответ на него можно получить, внимательно изучив таблицу 4.2. Таблица 4.2 Метод интегрирования по частям
Пример 4. Найти интегралы  Решение 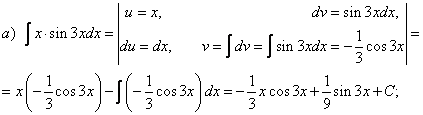 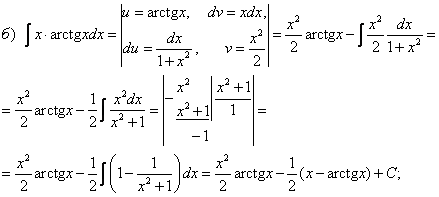 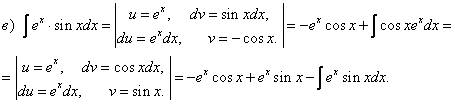 Обозначив получим J = –ex cos x + ex sin x – J.Выразим из последнего равенства J. 2J = –ex cos x + ex sin x. Следует отметить, что метод интегрирования по частям можно применять к одному интегралу несколько раз. Если это интеграл первой группы (таблица 4.2), то это зависит от степени многочлена Pn(x). Цит. по: Математика для средних специальностей / Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 92–99. 2.2. Интегрирование рациональных функций Определение 5.3.Функция называется рациональной, если ее можно представить в виде дроби  где P(x) и Q(x) — многочлены. Из класса всех дробей выделяют основные простые дроби:  где a, p, q, M, N ∈ R, k ∈ N. Интегралы от первых двух типов простых дробей находятся с помощью подстановки t = x - a:   Интеграл от третьего типа простых дробей рассмотрим в предположении, что знаменатель не имеет корней, т. е. q - p2 > 0. Выделим полный квадрат в знаменателе  где a2 = q - p2 > 0. 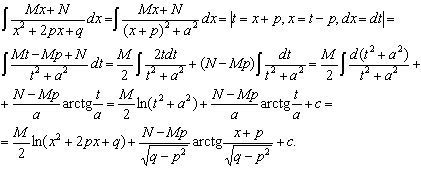 Если степень числителя выше степени знаменателя, то дробь называется неправильной; в таком случае выполнив деление, получим  где W(х) — некоторый многочлен, а второе слагаемое представляет собой правильную дробь, у которой степень числителя меньше степени знаменателя. Например, рассмотрим неправильную дробь  Разделим числитель на знаменатель 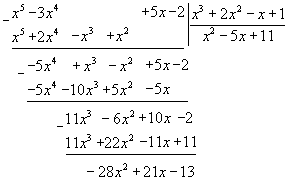 и выделим целую часть дроби  Целая часть дроби легко интегрируется. Следовательно, вопрос об интегрировании рациональной функции сводится к вопросу об интегрировании правильных дробей. Любую правильную дробь можно представить в виде суммы простых дробей с помощью следующих теорем. Теорема 5.10. Каждый многочлен Q(x) с действительными коэффициентами может быть представлен единственным образом в виде  где a, b, …, — корни многочлена кратности k, l,…; квадратичные множители кратности m, n, … не имеют действительных корней. Теорема 5.11. Пусть R(x)/Q(x) — правильная рациональная дробь, у которой знаменатель представлен в виде (5.1). Тогда эту дробь можно единственным образом представить в виде суммы простых дробей: 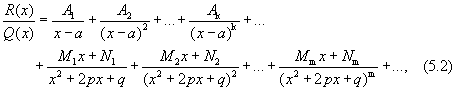 где  — некоторые действительные числа.Выражение (5.2) называется разложением рациональной дроби на простые дроби, числа  — коэффициентами разложения.Следствие. Пусть R(x)/Q(x) — правильная рациональная дробь, у которой знаменатель — многочлен степени n, имеющий n различных действительных корней a1, a2, …, an. Тогда эту дробь можно единственным образом представить в виде суммы простых дробей:  где A1, A2, …, An— некоторые действительные числа. Для определения коэффициентов разложения используют метод неопределенных коэффициентов, который состоит в следующем: приводят левую часть равенства (5.2) или (5.3) к общему знаменателю и приравнивают коэффициенты при одинаковых степенях многочлена, полученного в числителе и многочлена R(x). Пример 5.9. Разложим дробь 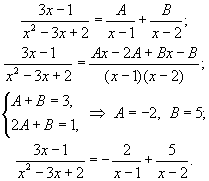 на простые дроби. Знаменатель имеет два корня — 1 и 2. Воспользуемся формулой (5.3). Пример 5.10. Разложим дробь 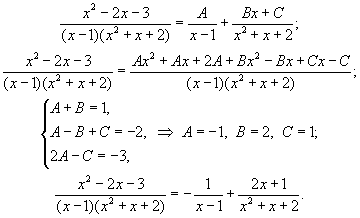 на простые дроби. Квадратичный множитель в знаменателе не имеет корней. Воспользуемся формулой (5.2). 2.3. Интегрирование дробно-линейных иррациональных функций 1.Рассмотрим интеграл от рациональной функции 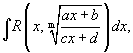 где a, b, c, d ∈ R , m ∈ N. Подынтегральная функция сводятся к рациональной функции заменой  Пример 5.11. 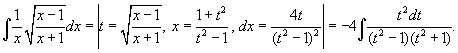 Подынтегральная функция представляет собой правильную рациональную дробь. 2.Интегралы вида  сводятся к табличным выделением полного квадрата в подкоренном выражении и заменой переменной. Пример 5.12. 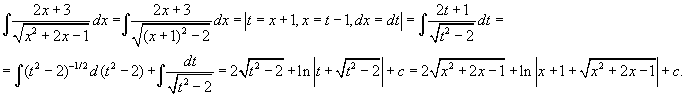 2.4. Интегрирование тригонометрических выражений Интегралы от произведений синуса и косинуса разных аргументов sinmx cosnx dx, sinmx sinnx dx, cosmx cosnx dx.Данные интегралы сводятся к табличным с помощью формул преобразования произведения в сумму: sin a cos  = 1/2(sin(a - ) + sin(a + )),sin a sin = 1/2(cos(a - ) - cos(a + )),cos a cos = 1/2(cos(a - ) + cos(a + )).Пример 5.13. 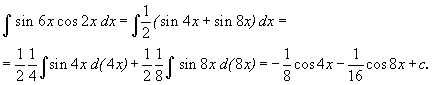 Интегралы от степеней синуса и косинуса одного аргумента sinm x cosn x dx.1. Если хотя бы одно из чисел m и n нечетно, то от нечетной степени отделяют один сомножитель и вносят его под знак дифференциала. Подынтегральную функцию приводят к одной из тригонометрических функций. Пример 5.14. sin5 x cos4 x dx = sin4 x cos4 x sin xdx= - (1 - cos2 x)2 cos4 x d(cosx) = - cos4 x d(cosx) + 2 cos6 x d(cosx) - cos8 x d(cosx) =  2. Обе степени четные. В этом случае применяют формулы понижения степени  до тех пор, пока не появятся нечетные степени тригонометрических функций. Интегралы от рациональной функции, содержащей синус и косинусРассмотрим интеграл вида  Этот интеграл рационализируется универсальной подстановкой 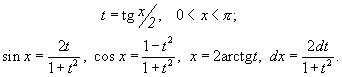 Пример 5.15. 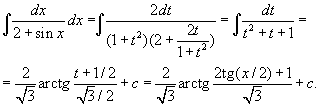 Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 70–76.
Цит. по: Высшая математика в схемах и таблицах / Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 54, 55. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
,
,