ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 11 из 32

Тема 3. Точки перегиба

3.1. Выпуклость, вогнутость, точки перегиба

Рассмотрим на плоскости хОу кривую y = f(x), являющуюся графиком дифференцируемой функции y = f(x) (рис. 3.7).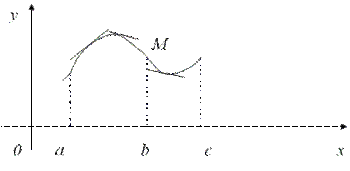



Рис. 3.7

Определение. Кривая y = f(x) называется выпуклой на интервале (a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Кривая y = f(x) называется вогнутой на интервале (b, c), если все точки кривой лежат выше любой ее касательной на этом интервале.

Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Направление выпуклости, вогнутости кривой является важной характеристикой ее формы.

Теорема 3.11 (достаточный признак выпуклости, вогнутости). Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f"(x₀) < 0, то кривая y = f(x) на этом выпукла. Если f"(x₀)> 0 на (a, b), то кривая y = f(x) – вогнута на (a, b).

Теорема 3.12 (достаточный признак существования точки перегиба). Если вторая производная f"(x) функции y = f(x) обращается в точке х ₀ в нуль или не существует и при переходе через эту точку меняет знак, то точка (х₀, f(x₀)) графика данной функции является точкой перегиба.

Определение. Точки области определения, в которых вторая производная функции y = f(x) обращается в нуль или не существует, называются критическими точками второго рода.

Пример 3. Найти промежутки выпуклости, вогнутости, точки перегиба функции y = x⁴ – 4x³ + 3.

Решение

1) D(y) = (– ;  ).

2) y' = 4x³ – 12x².

3) y'' = 12x² – 24x, y'' = 0 при 12x² – 24x = 12x (x – 2) = 0, x = 0 и x = 2.

Точки x = 0, – критические точки второго рода.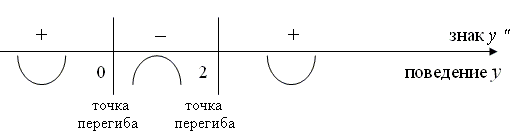



y(0) = 3, y(2) = –13.

3.2. Асимптоты

Определение. Прямая l называется асимптотой кривой (рис. 3.8), если расстояние от переменной точки М кривой до этой прямой стремится к нулю при удалении точки М в бесконечность (ρ   0 при М    ).



Рис. 3.8

Асимптоты бывают вертикальные (рис. 3.9), горизонтальные (рис. 3.10) и наклонные (рис. 3.11).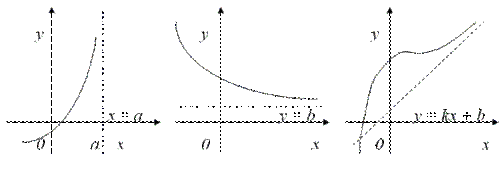



Рис. 3.9 Рис. 3.10 Рис. 3.11

Определение. Прямая х = а называется вертикальной асимптотой графика функции y = f(x), если

Вертикальные асимптоты могут проходить либо через точки разрыва функции, либо через граничные точки области определения.

Определение. Прямая y = kx + b называется наклонной асимптотой (при k = 0 горизонтальной асимптотой), если существуют пределы

Пример 4. Найти все возможные асимптоты к графику функции

Решение

1) D(y) = (– ; 5)   (5; + ), точка х = 5 является точкой разрыва. Следовательно, прямая х = 5 является вертикальной асимптотой.

Исследуем поведение функции вблизи точки разрыва слева и справа от нее.



2) Найдем наклонную асимптоту, для этого вычислим пределы (3.4) и (3.5) применительно к нашей функции



В итоге получили наклонную асимптоту с уравнением у = 2.

Замечание. 1. Если хотя бы один из пределов (3.4, 3.5) не существует, то линия y = f(x) наклонных асимптот не имеет.

1) Если существует асимптота при х   + , то ее называют правосторонней, если существует асимптота при х   – , то ее называют левосторонней.

2) Если при х   –  и при х   +  пределы (3.4) и (3.5) совпадают, то правосторонняя и левосторонняя асимптоты являются частями одной прямой.

Цит. по: Математика для средних специальностей /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 74–78.