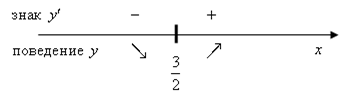ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 9 из 32

ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ

Тема 1. Возрастание (убывание) функций

Определение. Функция y= f(x) называется возрастающей на интервале (a, b), если для любых x₁ и x₂ из этого интервала, для которых x₁ < x₂, верно неравенство f(x₁) < f(x₂).

Определение. Функция y = f(x) называется убывающей на интервале (a, b), если для любых x₁ и x₂ из этого интервала, для которых x₁ < x₂, верно неравенство f(x₁) > f(x₂).

Необходимое условие возрастания функции. Если функция y= f(x) дифференцируема и возрастает на интервале (a, b), то f′(x) ≥ 0 для всех xиз этого интервала.

Необходимое условие убывания функции. Если функция y= f(x) дифференцируема и убывает на интервале (a, b), то f′(x) ≤ 0 для всех xиз этого интервала.

Достаточное условие возрастания (убывания функции). Пусть функция y= f(x) дифференцируема на интервале (a, b). Если во всех точках этого интервала f′(x) > 0, то функция возрастает на этом интервале, а если f′(x) < 0, то функция убывает на этом интервале.

Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. —
Режим доступа к курсу: http://e-college.ru. —П. 8.4.

Пример 1

Определить поведение функции y = –x² + 5x – 3 при х = –1.

План решения

1. Найти y'.

2. Определить знак y' в точке х = –1. Для этого вместо x в y' подставить –1.

3. Сделать вывод: если y'(–1) > 0, то в точке м функция возрастает, если y'(–1) < 0, то в точке х = –1 функция убывает.

Решение	Комментарий
y' = (–x2 + 5x – 3)' = – 2x + 5. y'(–1) = – 2(–1) + 5 = 2 + 5 = 7 > 0. Следовательно, в точке х = –1 функция возрастает.	Использовать формулы: (xn)' = nxn– 1; (Cx)' = C, C = const; C' = 0.

< …>

Пример 3

Найти промежутки возрастания или убывания функции y = 3x² – 9x + 2.

План решения

1. Найти область определения функции.

2. Найти y'.

3. Найти критические точки x₁, x₂ и т.д., т.е. точки области определения, в которых y' = 0. Нанести эти точки на числовую прямую. Получится несколько интервалов.

4. Определить знак y' в каждом полученном интервале и сделать вывод:

Решение	Комментарий
1. Область определения: D(y): (– ; + ), т.к. функция представляет собой многочлен. 2. y' = (3x2 – 9x + 2)' = 6x – 9. 3. y' = 0 при 6x – 9 = 0. Функция возрастает при   и убывает при.	Использовать формулы: (xn)' = nxn– 1; (Cx)' = C, C = const; C' = 0. Для определения знака y' в каждом интервале необходимо взять числа из каждого интервала и подставить в уравнение производной.

Цит. по: Методическое пособие-тренажер решения задач по высшей математике /
Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 44–45.