ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 7 из 32

Тема 2. Правило дифференцирования сложной функции

Производная сложной, неявно и параметрически заданной функции

Производная сложной функции

y= f(u), u=  (x) y'x= f'u   u'x, где u — промежуточный аргумент.

Производная функции, заданной неявно F(x; y) = 0

Продифференцировать уравнение F(x; y) = 0 по x, считая yфункцией от x. Разрешить полученное выражение относительно y'.

Производная функции, заданной параметрически

Логарифмическое дифференцирование

Прологарифмировать исходное уравнение y= f(x) (т. е. ln y = ln f(x)). Полученное выражение продифференцировать по x, считая yфункцией от х (т.е.  ) и выразить из него y'.

Производная второго порядка

Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 43.

Пример 5.9. Найти производные функций:









Решение: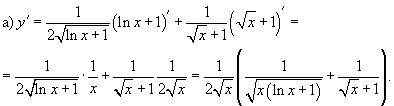



б) По правилу дифференцирования произведения двух функций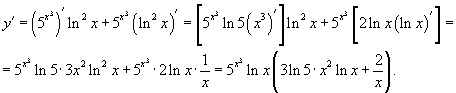



в) По правилу дифференцирования частного двух функций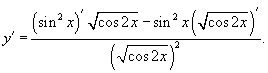



Учитывая, что (sin² х)' = 2 sin x(sin x)' = 2 sin xcos x= sin 2 x,



после преобразований получаем



г) Применяя метод логарифмического дифференцирования, находим вначале по формуле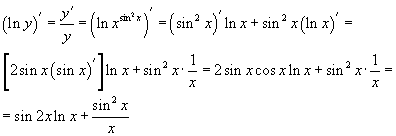



Теперь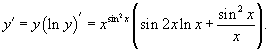



Пример 5.10. Найти производные функций у'_х:

а) е^y+ е^-х + ху = 0;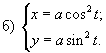



Решение, а) При дифференцировании неявно заданной функции учитываем, что у есть функция от х, получаем

e^y   y' + e^-x(-x)' + x'y + xy' = 0 или

e^y   y' -e^-x+ y + xy' = 0, откуда



б) Используя правило дифференцирования функций, заданных параметрически, получаем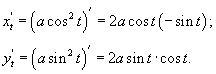



Отсюда



Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 164, 165.