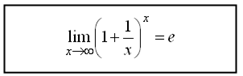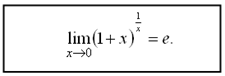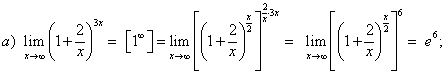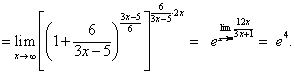ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 4 из 32

2.2. Свойства бесконечно малых

Теорема 1.1. Для того, чтобы число у₀ было пределом функции f(x) при х   х₀, необходимо и достаточно, чтобы эта функция была представима в виде f(x) = y₀ +  (x), где  (х) — бесконечно малая, т.е.

   f(x) = y₀ +  (x),  (х) — б.м.

Теорема 1.2. Еслифункция f(x) при х   х₀ — бесконечно большая, то функция   при х   х₀ — бесконечно малая.

Обратно, если функция f(x) при х   х₀– бесконечно малая, то функция   при х   х₀ — бесконечно большая.

Например, функция f(x) = 2x³ — б.м. при х   0, а функция   при х   0 — б.б.

Теорема 1.3. Алгебраическая сумма конечного числа бесконечно малых есть функция бесконечно малая.

Теорема 1.4. Произведение ограниченной при х   х₀ функции на бесконечно малую есть функция бесконечно малая.

Следствие 4.1. Произведение постоянной на бесконечно малую есть бесконечно малая.

Следствие 4.2. Произведение двух бесконечно малых есть бесконечно малая.

Теорема 1.5. Частное от деления бесконечно малой на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Определение. Если  (х) и  (х) – бесконечно малые функции и

то они называются эквивалентными при х   х₀.

Эквивалентные бесконечно малые обозначаются:

(х)   (х).

Теорема 1.6. Предел отношения двух бесконечно малых функций равен пределу отношения эквивалентных им функций, т.е. если при х   х₀  (х)   ₁(х),  (х)   ₁(х), то



2.3. Теоремы о пределах

Все рассматриваемые в этом параграфе предложения о пределах имеют место и при х   х ₀ и при х    .

Теорема 1.7 ("о двух милиционерах"). Если для функций f(x), f₁(x) и f₂(x) в некоторой окрестности точки х₀ выполняется неравенство f₁(x)   f(x)   f₂(x)

и 

Теорема 1.8. Если функция f(x)   0 (f(x)   0) для всех х в некоторой окрестности точки х₀, кроме, быть может, самой точки х₀, и в точке х₀ имеет предел, то 

Теорема 1.9. Предел постоянной величины равен самой постоянной, т.е.

Теорема 1.10. Если функции f₁(x) и f₂(x) имеют пределы при х   х₀, то при х   х₀ имеют пределы также их сумма f₁(x) ± f₂(x), произведение f₁(x) × f₂(x) и частное   при условии, что  , причем



Доказательство

Докажем равенство 1.1, все остальные утверждения доказываются аналогично.

Пусть







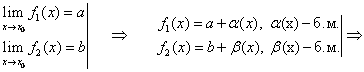
Следствие 10.1. Если функция f(x) имеет предел при х   х₀, то



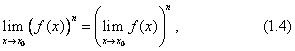
где n— натуральное число.

Следствие 10.2. Постоянный множитель можно выносить за знак предела:



Вычисление предела начинается с подстановки в выражение, стоящее под знаком предела, предельного значения аргумента. Если в результате подстановки получается какое-либо число или бесконечность, то задача считается решенной.

Пример 1. Вычислить пределы



Решение

На основании теоремы 1.10 имеем:





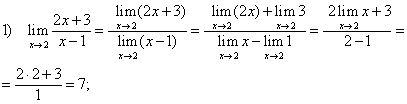
Однако теорема 1.10 не всегда позволяет вычислить предел. В тех случаях, когда  , то отношение   примет вид   и называется неопределенностью. Неопределенности бывают вида   Вычисление пределов для неопределенных выражений называется раскрытием неопределенностей. Каждая неопределенность имеет свое правило раскрытия. При вычислении пределов следует помнить:



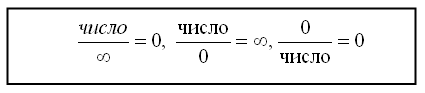
Раскрытие неопределенности вида 

Правило. Числитель и знаменатель дроби разделить на множитель, образующий их в нуль, т.е. при х   х₀ нужно делить на (х – х₀).

Пример 2. Вычислить пределы



Решение









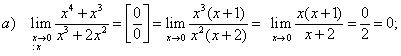
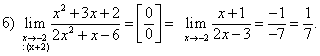
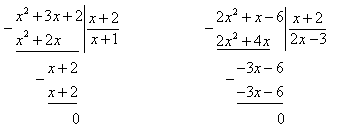
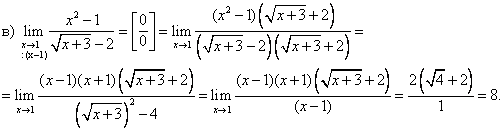
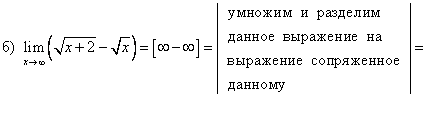
В данном примере, чтобы избавиться от неопределенности   числитель и знаменатель дроби умножили на выражение, сопряженное знаменателю.

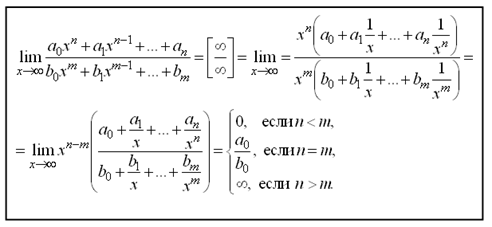
Раскрытие неопределенности вида 

Правило. Числитель и знаменатель дроби разделить на х в высшей степени.

Если под знаком предела стоит рациональная дробь, то вычисления можно значительно упростить.

Рассмотрим



Пример 3. Вычислить пределы:



Решение





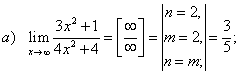
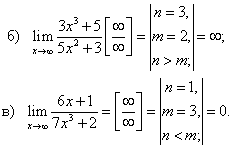
Пример 4. Вычислить 

Решение





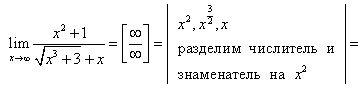
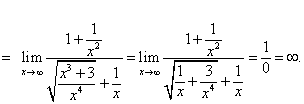
Раскрытие неопределенностей вида   и 

Правило. Представить исходное выражение в виде дроби.

Пример 5. Вычислить пределы



Решение









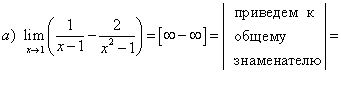
Цит. по: Математика для средних специальностей /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 17–29.

2.4. Непрерывность функции в точке

Пусть функция y = f(x) определена в некоторой окрестности точки х₀.

Определение 3.1.Функция y = f(x) называется непрерывной в точке х₀, если для любого   > 0 найдется   > 0 такое, что при всех х, удовлетворяющих неравенству |x - x₀| <  , будет выполняться неравенство

|f(x) - f(x₀)| <  .

Определение 3.2.Функция y = f(x) называется непрерывной на множестве А   R, если она непрерывна в каждой точке множества А.

Сравнивая определение 3.1 с определением предела функции, можно получить, что функция y = f(x) непрерывна в точке х₀ тогда и только тогда, когда ее предел при x   х₀ равен значению функции в этой точке:



Определение 3.3.Приращением аргумента называется разность двух значений переменной х и обозначается  х. Приращением функции, соответствующим данному приращению аргумента, называется разность двух значений функции от соответствующих аргументов и обозначается  у:

х = х - х₀,  у = f(x) - f(x₀).

Из определения 1 следует:





Таким образом, функция непрерывна в точке тогда и только тогда, когда малому приращению аргумента соответствует малое приращение функции.

2.5. Свойства функций, непрерывных на множестве

Теорема 3.1.Сумма и произведение конечного числа непрерывных на некотором множестве функций есть функция, непрерывная на этом множестве.

Доказательство (следует из основных теорем о пределах).

Пусть f(x) и g(x) — непрерывны в точке х₀, тогда



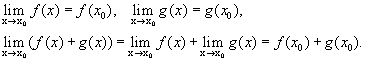
Следовательно, функция y = f(x) + g(x) непрерывна в точке х₀.

Доказательство для произведения функций проводится аналогично.

Теорема 3.2.Частное от деления двух непрерывных на множестве функций есть функция, непрерывная во всех точках, в которых знаменатель отличен от нуля.

Теорема 3.3(теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном множестве функция достигает на нем своего наибольшего и наименьшего значений.

2.6.Точки разрыва функции

Функция является непрерывной в точке, если



Определение 3.4.Точки, в которых нарушается условие непрерывности, называют точками разрыва функции.

Определение 3.5.Точка разрыва х₀ называется точкой разрыва первого рода, если существуют конечные односторонние пределы в этой точке.

Определение 3.6.Точка разрыва первого рода называется точкой устранимого разрыва, если односторонние пределы в этой точке равны.

Определение 3.7.Скачком функции в точке разрыва первого рода называется модуль разности односторонних пределов в этой точке.

Определение 3.8.Точка х₀ называется точкой разрыва второго рода, если она не является точкой разрыва первого рода (если хотя бы один из односторонних пределов не существует или равен +   (- )).

Пример 3.1.



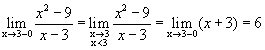
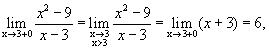 х = 3 — точка устранимого разрыва.



Функцию можно доопределить до непрерывной функции:

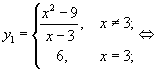 y = x + 3— непрерывная функция.

Пример 3.2.



y = [x] — целая часть числа.

Рассмотрим точку х = 1.



Следовательно, х = 1 — точка разрыва первого рода, скачок в ней равен единице.

Пример 3.3. Рассмотрим функцию   в точке х = 0.





 

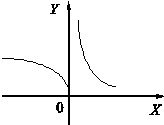
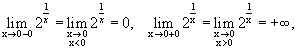
Следовательно, х = 0 — точка разрыва второго рода.

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 36–39.

2.7. Замечательные пределы

Первым замечательным пределом называется предел вида

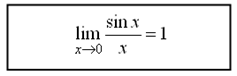 (1.6)

Следствия из первого замечательного предела:



Первый замечательный предел и его следствия используются для раскрытия неопределенности вида   в тех случаях, когда выражение, стоящее под знаком предела, содержит тригонометрические функции.

Так как функции х, sin x, tg x, arcsin x, arctg x при х   0 являются бесконечно малыми, то на основании первого замечательного предела и его следствий можно записать следующие соотношения

sin ax  ax при х   0,

tg ax  ax при х   0,

arcsin ax  ax при х   0,

arctg ax  ax при х   0.

Использование этих эквивалентностей значительно упрощает вычисление пределов в ряде случаев.

Пример 1. Вычислить пределы



Решение



Вторым замечательным пределом называется предел вида

 (1.7)

Второй замечательный предел может быть записан так:

 (1.8)

е — иррациональное число, е   2,718281…

Число е — одна из наиболее часто встречающихся величин. Показательная функция y = e^axназывается экспоненциальной или экспонентой. Логарифмы с основанием е называются натуральными и обозначаются символом ln, т.е.

log_e x = ln x.

Второй замечательный предел используется для раскрытия неопределенности |1 |.

Пример 2. Вычислить пределы:



Решение







Цит. по: Математика для средних специальностей /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 29–31.