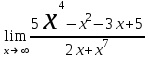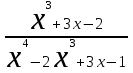Главная страница
Навигация по странице:

  • Раздел 6. Элементы математического анализа

  • Раздел 7.

  • Раздел 8. Геометрия

  • Методические рекомендации

  • Используя методические рекомендации, выполните задания

  • Самостоятельная работа № 11.

    		•

    самостоятельные работы 2 курс. Самостоятельные 2 семестр. Содержание самостоятельной работы


    Скачать 1.81 Mb.
    НазваниеСодержание самостоятельной работы
    Анкорсамостоятельные работы 2 курс
    Дата13.02.2022
    Размер1.81 Mb.
    Формат файлаdocx
    Имя файлаСамостоятельные 2 семестр.docx
    ТипУрок
    #360195
    страница1 из 3
      1   2   3

    Содержание самостоятельной работы

    №
    № урока
    Наименования разделов и тем
    Кол.

    Час.
    Вопросы для изучения
    Формы самостоятельной работы

    Раздел 6. Элементы математического анализа

    10
    53
    Понятие предела функции в бесконечности. Асимптоты графика функции. Сравнение бесконечно малых и бесконечно больших. Свойства непрерывных функций. Теорема Вейерштрасса.
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    11
    56
    Применение производной в физике. Построение графиков функций с помощью производных
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    12
    57
    Применение производной при решении задач. Нахождение экстремумов функций нескольких переменных
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    13
    70
    Вычисление площадей плоских фигур и объемов тел вращения с помощью интеграла.
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    Раздел 7. Вероятность и статистика, логика, теория графов и комбинаторика

    14
    74
    Вероятностное пространство. Аксиомы теории вероятностей. Гипергеометрическое распределение и его свойства. Показательное распределение, его параметры. Распределение Пуассона и его применение. Кодирование. Двоичная запись.
    4

    1. Определение вероятностного пространства.

    2. Аксиомы теории вероятностей.

    3. Гипергеометрическое распределение и его свойства.

    4. Показательное распределение, его параметры.

    5. Распределение Пуассона и его применение.

    6. Кодирование. Двоичная запись. Примеры
    1.Конспект

    2.Сообщение

    15
    75
     Неравенство Чебышева. Теорема Чебышева и теорема Бернулли. Закон больших чисел. Центральная предельная теорема. Выборочный метод измерения вероятностей. Роль закона больших чисел в науке, природе и обществе.
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    16
    76
    Выборочный коэффициент корреляции. Линейная регрессия. Статистическая гипотеза. Статистика критерия и ее уровень значимости. Проверка простейших гипотез. Эмпирические распределения и их связь с теоретическими распределениями. Ранговая корреляция
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    17
    77
    Построение соответствий. Инъективные и сюръективные соответствия. Биекции. Дискретная непрерывность. Принцип Дирихле. Основные понятия теории графов. Деревья. Двоичное дерево. Связность. Компоненты связности. Пути на графе. Эйлеровы и Гамильтоновы пути.
    4

    1. Построение соответствий.

    2. Инъективные и сюръективные соответствия.

    3. Биекции. Дискретная непрерывность.

    4. Принцип Дирихле.

    5. Основные понятия теории графов.

    6. Деревья. Двоичное дерево. Связность.

    7. Компоненты связности.

    8. Пути на графе.

    9. Эйлеровы и Гамильтоновы пути.
    1.Конспект

    2.Сообщение

    Раздел 8. Геометрия

    18
    83
    Понятие об аксиоматическом методе. Теорема Менелая для тетраэдра. Методы нахождения расстояний между скрещивающимися прямыми. Геометрические места точек в пространстве.
    4

    1. Методы нахождения расстояний между скрещивающимися прямыми.

    2. Геометрические места точек в пространстве.
    Презентация

    19
    93
    Виды тетраэдров. Ортоцентрический тетраэдр, каркасный тетраэдр, равног-ранный тетраэдр. Прямоугольный тетраэдр. Медианы и бимедианы тетраэдра. Достраивание тетраэдра до параллелепипеда
    4

    1. Виды тетраэдров.

    2. Ортоцентрический тетраэдр, каркасный тетраэдр, равногранный тетраэдр.

    3. Прямоугольный тетраэдр.

    4. Медианы и бимедианы тетраэдра.

    5. Достраивание тетраэдра до параллелепипеда
    Презентация

    20
    95
    Площадь ортогональной проекции. Перпендикулярное сечение призмы.
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    21
    97
    Трехгранный и многогранный угол. Свойства плоских углов многогранного угла. Свойства плоских и двугранных углов трехгранного угла. Теоремы косинусов и синусов для трехгранного угла.
    4

    1. Трехгранный и многогранный угол.

    2. Свойства плоских углов многогранного угла.

    3. Свойства плоских и двугранных углов трехгранного угла.

    4. Теоремы косинусов и синусов для трехгранного угла.
    1.Конспект

    2.Сообщение

    3. презентация

    22
    99
    Развертки многогранника. Кратчайшие пути на поверхности многогранника. Теорема Эйлера. Двойственность правильных многогранников.
    4

    1. Развертки многогранника.

    2. Кратчайшие пути на поверхности многогранника.

    3. Теорема Эйлера.

    4. Двойственность правильных многогранников.

    1. Макет

    2. Презентация




    23
    102
    Элементы сферической геометрии. Конические сечения. Касающиеся сферы. Комбинации тел вращения.
    4

    1. Элементы сферической геометрии.

    2. Конические сечения. Касающиеся сферы.

    3. Комбинации тел вращения.
    1.Конспект

    2.Презентация

    3. реферат

    24
    105
    Развертка цилиндра и конуса.
    2
    1.Способы построения цилиндра и конуса.

    2.Развертка цилиндра и конуса.
    1.презентация

    25
    109
    Аксиомы объема. Вывод формул объемов прямоугольного параллелепипеда, призмы и пирамиды. Формулы для нахождения объема тетраэдра. Теоремы об отношениях объемов.
    4

    1. Аксиомы объема.

    2. Вывод формул объемов прямоугольного параллелепипеда, призмы и пирамиды.

    3. Формулы для нахождения объема тетраэдра.

    4. Теоремы об отношениях объемов.
    1.Конспект

    2.Презентация

    3. реферат

    26
    111
    Приложения интеграла к вычислению объемов и поверхностей тел вращения
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    27
    112
    Площадь сферического пояса. Объем шарового слоя. Применение объемов при решении задач.
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    28
    114
    Движения в пространстве: параллельный перенос, симметрия относительно плоскости, центральная симметрия, поворот относительно прямой. Преобразование подобия, гомотетия
    4

    1. Параллельный перенос в пространстве.

    2. Виды симметрии.

    3. Преобразование подобия, гомотетия
    Презентация

    29
    116
    Решение задач на плоскости с использованием стереометрических методов
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    30
    118
    Решение задач с помощью векторов и координат. Формула расстояния от точки до плоскости. Способы задания прямой уравнениями.
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы

    31
    119
    Решение задач и доказательство теорем с помощью векторов и методом координат. Элементы геометрии масс.
    4
    Домашняя контрольная работа
    Выполнение заданий контрольной работы







    Итого:
    122








    Самостоятельная работа № 10.

    Тема: Понятие предела функции в бесконечности. Асимптоты графика функции. Сравнение бесконечно малых и бесконечно больших. Свойства непрерывных функций. Теорема Вейерштрасса.

    Цель: научиться вычислять предел функции

    Методические рекомендации

    Пример 1. Вычислить предел

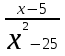
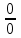    Решение: При подстановке вместо переменной х числа 5 видим, что получается неопределенность вида . Для ее раскрытия нужно разложить знаменатель на множители: х2 -25 = (х-5)*(х+5), получили общий множитель (х-5),на который можно сократить дробь. Задан­ный предел примет вид: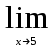 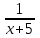. Подставив х=5,получим результат: = = =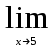

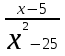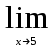
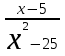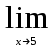
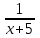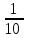
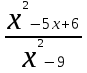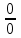    Пример 2. Вычислить предел .

    Решение: При подстановке вместо переменной х числа 3 видим, что получается неопределенность вида . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель х-3. В результате получим новый предел, знаменатель ко­торого при подстановке вместо переменной х числа 3 не равен нулю. Этот предел легко вы­числяется по теоремам. Таким образом, неопределенность будет раскрыта.


    Пример 3. Вычислить предел

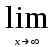
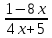
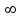    Решение: При подстановке вместо переменной х бесконечности ( ) видим, что получается неопределенность вида 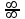. Для ее раскрытия нужно числитель и знаменатель разделить на наивысшую степень, в данном случае на х. Получим: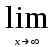

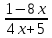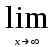
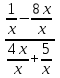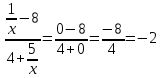    = = , т.к. величины 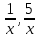являются бесконечно малыми и их пределы равны 0.

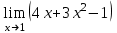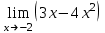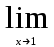
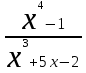
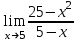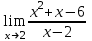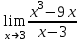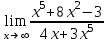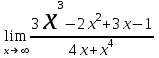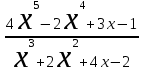
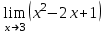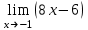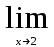
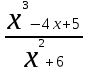
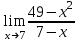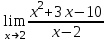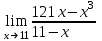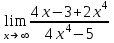    Используя методические рекомендации, выполните задания:

    1 вариант
    2 вариант

    Вычислите пределы:

    1) ;

    2) ;

    3)

    4) ;

    5) ;

    6) ;

    7) ;

    8) ;

    9)

    1) ;

    2) ;

    3)

    4) ;

    5) ;

    6) ;

    7) ;

    8)

    9)


    Самостоятельная работа № 11.

      1   2   3

    написать администратору сайта