самостоятельные работы 2 курс. Самостоятельные 2 семестр. Содержание самостоятельной работы
 Скачать 1.81 Mb. Скачать 1.81 Mb.
|
|
Тема: Применение производной в физике. Построение графиков функций с помощью производных Цель: научиться применять производную при решении задач по физике, исследовать функцию с помощью производной и строить графики функций. Методические рекомендации: Пример 1. Материальная точка движется прямолинейно по закону x(t) = t2 – 7t – 20, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t= 5 c. Решение: Физический смысл производной это скорость (скорость движения, скорость изменения процесса, скорость работы и т.д.) Найдем закон изменения скорости: v (t) = x′(t) = 2t – 7 м/с. При t = 5 имеем: Ответ: 3 Пример 2. Материальная точка движется прямолинейно по закону x(t)=(1/6)t2+5t+28, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с? Решение: Найдем закон изменения скорости: Для того, чтобы найти, в какой момент времени t скорость была равна 6 м/с, необходимо решить уравнение: Ответ: 3 Пример 3. Исследовать функцию 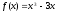 и построить ее график: и построить ее график:Решение: 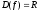 . . Функция нечетная, т.к. 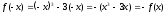 . Следовательно, она симметрична относительно начала координат. . Следовательно, она симметрична относительно начала координат.Точки пересечения графика с осью ОХ: 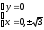 ; ;Точки пересечения графика с осью ОY: 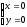 . .Исследуем функцию на монотонность и точки экстремума: 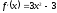 , , 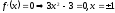 Функция возрастает на 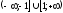 ; функция убывает на ; функция убывает на 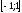 . .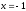 - точка максимума, - точка максимума, 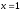 - точка минимума. - точка минимума.
Построим график функции:  Используя предложенные методические рекомендации, выполните задания: Материальная точка движется прямолинейно по закону x (t) = 6t2 – 48t + 17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 c. 2. Материальная точка движется по прямой так, что ее координата в момент времени t равна x(t)=t3-2t2. Найдите ускорение точки в момент времени t=3. 3. Исследовать функции у = х2 - 1 и построить график. Самостоятельная работа № 12 Тема: Применение производной при решении задач. Нахождение экстремумов функций нескольких переменных Цель: научиться применять производную при решении задач, Методические рекомендации: ПРИМЕР 1. Тело движется по прямой согласно закону РЕШЕНИЕ. Скорость движения – это производная от пути по времени, следовательно, Значит, в момент времени О т в е т: 46. ПРИМЕР 2. Точка движется по закону Решение: Скорость это производная пути по времени. Значит: Подставив значение времени получим Пример 3. Тело движется прямолинейно по закону Решение: Формула нахождения кинетической энергии: Найдем скорость тела. Кинетическая энергия тела составит: Пример 4. Зависимость пройденного телом пути от времени задается уравнением s=A+Bt+Ct2+Dt3 (C=0,1 м/с, D = 0,03 м/с2). Определить время после начала движения, через которое ускорение тела будет равно 2 м/с2. Решение: v(t) = s'(t) = B + 2Ct + 3Dt2; a(t) = v'(t) = 2C + 6Dt = 0,2 + 0,18t = 2; 1,8 = 0,18t; t = 10 c Используя предложенные методические рекомендации, выполните задания:
Самостоятельная работа № 13 Тема: Вычисление площадей плоских фигур и объемов тел вращения с помощью интеграла. Цель: научиться вычислять площадь криволинейной трапеции с помощью формулы Ньютона - Лейбница Методические указания Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f (x), снизу — осью Ох, слева и справа прямыми х=a, x=b, находят по формуле Ньютона-Лейбница: 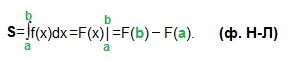 Пример 1. Вычислить площадь фигуры, ограниченной осью Ох и графиком функции у=х2-2х при 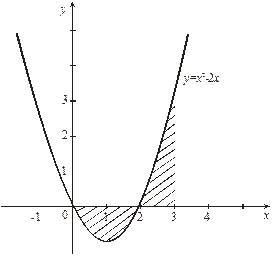 Решение. Сделаем чертеж. Искомая площадь представляет собой сумму площадей и . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему 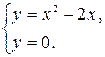 Получим , . Получим , . Следовательно: 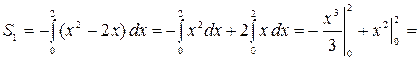 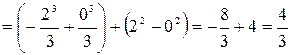 ; ;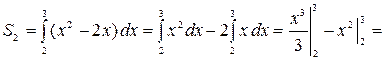 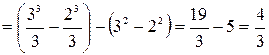 . .Τᴀᴋᴎᴍ ᴏбᴩᴀᴈᴏᴍ, площадь заштрихованной фигуры равна Пример 2. Вычислить площадь фигуры, ограниченной линиями у = -х2 - 1, у = 0, х = -1, х = 2. Решение: 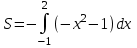 = -( = -(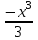 - х) - х) 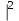 -1 = -( -1 = -(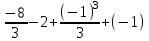 ) = 6 кв.ед. ) = 6 кв.ед.Используя предложенные методические рекомендации, выполните задания: Вычислить площадь фигур, ограниченных линиями:
Самостоятельная работа № 15 Тема: Неравенство Чебышева. Теорема Чебышева и теорема Бернулли. Закон больших чисел. Центральная предельная теорема. Выборочный метод измерения вероятностей. Роль закона больших чисел в науке, природе и обществе. Цель: научится решать задачи вычисления вероятности используя формулы теоремы Бернулли. Методические указания Схема Бернулли. Формула Бернулли Пусть производится n независимых однотипных испытаний, в каждом из которых событие А может появиться с вероятностью Р. Тогда вероятность не появления события А, т.е. Р( 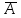 ) равна q=1-p. ) равна q=1-p. Вероятность того, что событие А произойдет в этих n независимых испытаниях ровно k раз, можно вычислить по формуле Бернулли 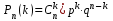 Для определения вероятности появления события A менее m раз (k < m), более m раз (k > m), хотя бы один раз ( 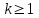 ) и т. п. могут быть использованы формулы: ) и т. п. могут быть использованы формулы: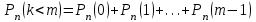 , ,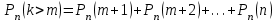 , ,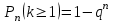 . .Пример 1: Прибор состоит из пяти узлов. Надежность (вероятность безотказной работы в течение времени t) для каждого узла равна 0,9. Узлы выходят из строя независимо один от другого. Найти вероятность того, что за время t откажут ровно два узла. Решение: выхода узла из строя: p =P(A)=0,1. Тогда q=1-p=1-0,1=0,9. Теперь вычислим искомую вероятность по формуле Бернулли: Р5(2) = 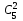 (0,1)2 .(0,9)3=10.0,01.0,729=0,072 (0,1)2 .(0,9)3=10.0,01.0,729=0,072Рассмотрим событие А - выход узла из строя за время t. Число узлов n=5. Число отказавших узлов за время t: k=2. Р(А) - вероятность 9. Пример 2: Всхожесть семян данного растения равна 90 %. Найти вероятность того, что из четырех посеянных семян взойдут: а) три; б) не менее трех. Решение а) Искомую вероятность находим с помощью формулы Бернулли (14), учитывая что 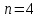 , , 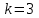 , , 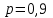 , , 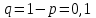 . .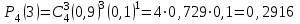 . .б) «Не менее трех» означает, что из четырех семян взойдут или три, или четыре. Так как эти события несовместны, то по теореме сложения искомая вероятность равна 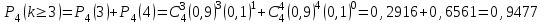 . .Предельные теоремы для схемы Бернулли Теорема Пуассона. (Отметим, что на практике эта теорема применяется при 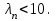 Это означает, что p должно быть очень малым числом). Пусть имеется n независимых испытаний с вероятностью р успеха в одном испытании и q- вероятностью неудачи. Тогда для любого фиксированного m справедливо соотношение Это означает, что p должно быть очень малым числом). Пусть имеется n независимых испытаний с вероятностью р успеха в одном испытании и q- вероятностью неудачи. Тогда для любого фиксированного m справедливо соотношение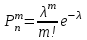 , где , где 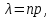 Пример 1: Машинистка печатает текст, который содержит 20000 знаков. Каждый знак может быть напечатан неправильно с вероятностью 0.0004. Какова вероятность того, что в тексте не менее 3 опечаток? Решение. Если опечатку считать успехом, то к этой задаче применима схема Бернулли при p=0.0004, n=20000. Поскольку λ=np=8, то можно использовать предельную теорему Пуассона. Поэтому, искомая вероятность равна 1-Pn0- Pn1- Pn2=1-e-8- 8 e-8-(64/2) e-8= 1-41 e-8=0.986. Пример 2: Монета бросается 100 раз. Найти приближенно вероятность того, что герб выпадет 40 раз. (Воспользоваться таблицей ) Решение. Если считать успехом выпадение герба, то вероятность успеха равна 1/2. Поэтому используя предельную локальную теорему Муавра-Лапласа, получим 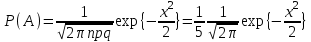 , где , где 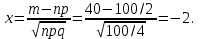 Таким образом, используя таблицы для плотности нормального распределения, получим P(A)=0.0108. Интегральная теорема Муавра-Лапласа. Пусть имеется n независимых испытаний с вероятностью успеха p, 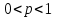 , в одном испытании и , в одном испытании и 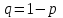 - вероятностью неудачи. Величина - вероятностью неудачи. Величина 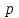 не зависит от n. Тогда .для любых вещественных чисел a<b при не зависит от n. Тогда .для любых вещественных чисел a<b при 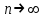 P(a< 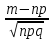 <b )=Φ(b)- Φ(a). <b )=Φ(b)- Φ(a).Здесь Φ(x)= 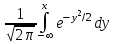 - функция Лапласа, значения которой заданы в таблицах, приведенных в большинстве задачников по вероятности и математической статистике. - функция Лапласа, значения которой заданы в таблицах, приведенных в большинстве задачников по вероятности и математической статистике. Пример 1: При рождении ребенка вероятность рождения мальчика равна 0.512. Найти вероятность того, что среди 1000 новорожденных мальчиков родится больше, чем девочек. Решение. Пусть A – это событие, соответствующее вопросу задачи, m – это число рожденных мальчиков. Нетрудно видеть, что P(A) = P(m>500). Поскольку n=1000 можно считать достаточно большим, то применим интегральную теорему Муавра-Лапласа, согласно которой P(A)=P( 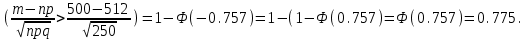 Используя методические рекомендации, решите задачи: Вариант 1 В магазин поступила партия лампочек, среди них 3 % составляет брак. Найти вероятность того, что из 5 купленных лампочек 4 будут хорошими. Вероятность изготовления на автоматическом станке бракованной детали равна 0,1. Какова вероятность того, что из четырех деталей бракованных окажется не более двух? Вариант 2 При установившемся технологическом процессе автомат производит 0,75 числа деталей первого сорта и 0,25 – второго. Установить, что является более вероятным – получить 3 первосортных детали среди 5 наудачу отобранных или 4 первосортных среди 6 наудачу отобранных? Среди изделий, произведенных а станке-автомате, в среднем бывает 90 % изделий первого сорта. Какова вероятность того, что среди 5 наудачу выбранных изделий будет не менее 4 первого сорта? Самостоятельная работа № 16 Тема: Выборочный коэффициент корреляции. Линейная регрессия. Статистическая гипотеза. Статистика критерия и ее уровень значимости. Проверка простейших гипотез. Эмпирические распределения и их связь с теоретическими распределениями. Ранговая корреляция. Цель: получить навыки по записи распределения ДСВ, заданной содержательным образом Методические рекомендации Пример построения ряда распределения ДСВ Пример: Два стрелка стреляют по мишени, делая по два выстрела каждый. Вероятность попадания в мишень при каждом выстреле для первого стрелка равна 0,7, а для второго - 0,6. Построить ряд распределения случайной величины Х – общего числа попаданий в мишень. Найти числовые характеристики этой случайной величины. Решение: Случайная величина Х - общее число попаданий в мишень может принимать следующие значения: х1=0, х2=1, х3=2, х4=3, х5=4. Случайная величина Х примет значение х1=0. когда произойдет событие С - ни один из стрелков не попал в мишень. Событие С произойдет в том случае, если одновременно произойдут следующие четыре события: А1 - 1-й стрелок не попал в мишень при первом выстреле; А2 - 1-й стрелок не попал в мишень при втором выстреле; В1 - 2-й стрелок не попал в мишень при первом выстреле; В2 - 2-й стрелок не попал в мишень при втором выстреле. Отсюда следует: что событие С равно произведению независимых событий А1, А2, В1, В2. С= А1 .А2 .В1 .В2. Откуда Р(С)=Р(А1).Р(А2).Р(В1).Р(В2). По условию задачи 1-й стрелок попадает в мишень вероятностью 0,7, а 2-й - с вероятностью 0,6. Тогда вероятности непопадании в мишень для каждого стрелка будут следующими: Р(А1) =Р(А2)=1-0,7=0,3; Р(В1 )=Р(В2)=1-0,6=0,4. Вероятность того, что случайная величина Х примет значение х1 = 0, равна вероятности события С: Р(Х=0)=Р(С)=0,3 .0,3 .0,4 .0,4=0,0144. Аналогично подсчитываем и другие вероятности: Р(Х=1)=0,7.0,3.0,4 .0,4+0,3.0,7.0,4 .0,4+0,3.0,3.0,6.0,4+0,3.0,3.0,4 . .0,6=0,1104. Р(Х=2)=0,7.0,7.0,4 .0,4+0,3 .0,3 .0,4 .0,4+4 .(0,7 .0,3 .0,6 .0,4)=0,3124. Р(Х=3)=0,3.0,7.0,6.0,6+0,7.0,3.0,6.0,6+0,7.0,7.0,4.0,6+0,7.0,7.0,6.0,4==0,3864. Р(Х=4)=0,7 .0,7 .0,6 .0,6=0,1764. Составим ряд распределения случайной величины Х.
Проверим тождество 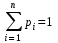 . .0,0114+0,1104+0,З124+0,3864+0,1764 =1. Используя методические рекомендации, решите задачи: Связь с дрейфующей станцией могут поддерживать три радиостанции. Вступает с ней в двустороннюю связь та радиостанция, которая первая примет позывные дрейфующей станции. Причем принять сигналы дрейфующей станции для каждой радиостанции имеет одну и ту же вероятность, равную 1/3. Дрейфующая станция будет устанавливать связь 4 раза в сутки. Составить ряд распределения случайной величины - числа вступлений в двустороннюю связь для радиостанции №1. Вероятность изготовления нестандартной детали равна 0,1. Для проверки на качество ОТК берет из партии не более четырех деталей. При обнаружении нестандартной детали вся партия задерживается. Составить ряд распределения числа подвергшихся проверке деталей. В цехе брак составляет 5% всех изделий. Составить ряд распределения числа бракованных изделий из трех взятых наудачу. Самостоятельная работа № 20 Тема: Площадь ортогональной проекции. Перпендикулярное сечение призмы. Цель: научиться определять ортогональные проекции отрезков, площадь ортогональной проекции многоугольников. Методические указания 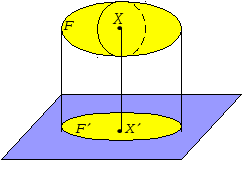   Используя методические рекомендации, выполните задания: В результате ортогонального проектирования: - проекцией квадрата может быть квадрат; - проекцией квадрата может быть прямоугольник с неравными сторонами; - проекцией куба может быть квадрат; - проекцией тетраэдра может быть треугольник; - проекцией шара может быть не круг. Найдите ортогональные проекции диагонали BD1 куба ABCDAB1С1D1 на грани: 1) ABCD; 2) A1B1С1D1; 3) DD1С1C ; 4) ADD1A1. 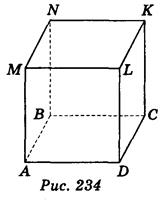 3. Вычислить площадь проекции правильного шестиугольника со стороной 8 см, плоскость которого наклонена к плоскости проекции под углом 450. Самостоятельная работа № 26 Тема: Приложения интеграла к вычислению объемов и поверхностей тел вращения Цель: научить вычислять объём поверхностей тел вращения с помощью определённого интеграла. Методические рекомендации Вычисление объемов тел вращения. Если тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной кривой 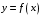 , осью OX и прямыми , осью OX и прямыми 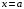 , , 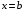 (рис. 2), то его объем вычисляется по формуле: (рис. 2), то его объем вычисляется по формуле: 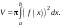
Пример 1. Найти объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями: 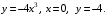 Решение. Построим криволинейную трапецию, вращением которой получается тело вращения.
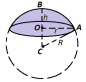
Используя методические рекомендации, выполните задания: Найти объем тела, полученного вращением вокруг оси ОХ фигуры, ограниченной линиями. 1) х2 - у = 0, у = 1 2) х2 +у = 0, у = -1 3) х – у2 = 0, х = 1 Самостоятельная работа № 27 Тема: Площадь сферического пояса. Объем шарового слоя. Применение объемов при решении задач Цель: научить вычислять объём поверхностей тел вращения с помощью определённого интеграла. Методические рекомендации Шаровой сегмент – часть шара, отсекаемая плоскостью (рис. 5). 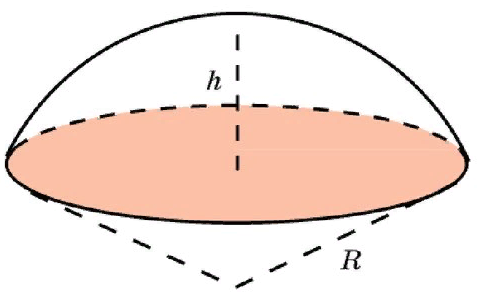 Рис. 5 Аналогично определяется понятие сферического сегмента. Площадь сферического сегмента называется шаровым сводом и находится по формуле 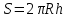 Шаровой слой – часть шара, заключенная между параллельными секущими плоскостями (рис. 6). 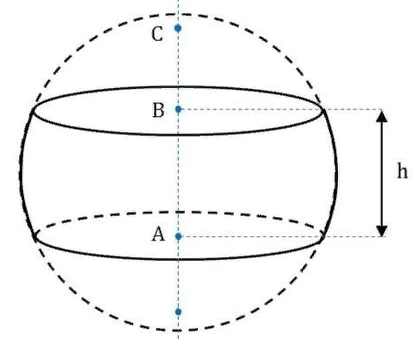 Рис. 6 Сферическая поверхность шарового слоя называется сферическим поясом. Его площадь вычисляется по формуле 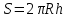 Шаровой сектор – часть шара, образованная вращением кругового сектора вокруг оси, проходящей через его центр (рис. 7). 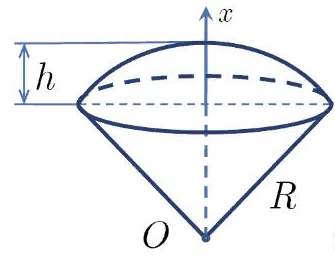 Рис. 7 Рис. 7Площадь поверхности шарового сектора определяется по формуле 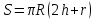 Пример 1. Площадь поверхности шарового сегмента вместе с площадью его основания равна  . Найдите высоту сегмента, если радиус шара равен . Найдите высоту сегмента, если радиус шара равен  . .
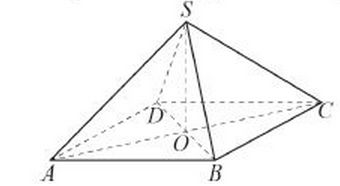
Используя методические рекомендации, выполните задания: Сечение шара имеет площадь 64π дм2 и удалено от центра шара на 6 дм. Найдите площадь поверхности сферы. Найдите площадь сферического пояса если радиусы его основы 20м и 24м, а радиус сферы 25м. Самостоятельная работа № 29 Тема: Решение задач на плоскости с использованием стереометрических методов Цель: закрепить умения решать задачи на плоскости с использованием стереометрических методов Методические рекомендации Пример 1. В правильной четырёхугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=12, AC=18. Найдите боковое ребро SB.
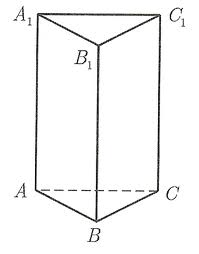
Пример 2. Дано: АВСС1В1А1 треугольная призма, прямая, правильная, АВ=ВС=АС = 5 см, Н = 10 см. Найти: Sб.п., Sп.п.
Используя методические рекомендации, выполните задания: В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковой грани к плоскости основания равен 60°. Найдите боковое ребро пирамиды. Диагональ AC основания правильной четырёхугольной пирамиды SABCD равна 6. Высота пирамиды SO равна 4. Найдите длину бокового ребра SB . Вычислите полную поверхность правильного тетраэдра, ребро которого 8 см. Самостоятельная работа № 30 Тема: Решение задач с помощью векторов и координат. Формула расстояния от точки до плоскости. Способы задания прямой уравнениями. Цель: научится составлять уравнения плоскости, определять расстояние от точки до плоскости, определять координаты векторов, скалярное произведение векторов. Методические рекомендации Пример 1. Составить уравнение плоскости по точке и вектору нормали . Решение: Используем формулу: 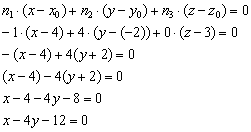 Ответ: Пример 2. Написать уравнение плоскости, проходящей через точку А перпендикулярно вектору . Решение. Если даны координаты начала и конца , то можем найти координаты вектора , вычитая координаты начала из координат конца. То есть . Подставляя координаты точек, получим Уравнение плоскости, проходящей через точку перпендикулярно вектору , имеет вид Подставляя найденные значения и координаты точки , получим или . Ответ: Уравнение искомой плоскости . Пример 3. Найти расстояние от точки до плоскости Решение: 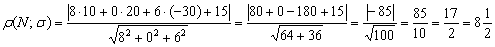 Ответ: Пример4. Вычислить скалярное произведение векторов, если их длины соответственно равны 2 и 3, а угол между ними 60°. Решение. Так как из условия , , а Используя методические рекомендации, выполните задания: Задача 1. Составить уравнение плоскости, проходящей через точку: а) M(1;-2;3) с заданным нормальным вектором N=(1;2;-3) б) M(-1;2;3) с заданным нормальным вектором N=(1;-2;-3) Задача 2. Найти расстояние от точки до плоскости а) M(1;0;2), 2x-y+2z=9 б) M(-1;1;2) до плоскости x- 2y+2z+2=0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

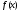
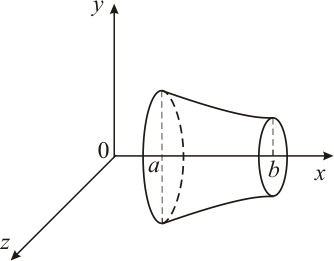
 тела, полученного вращением фигуры ОАВС, вычтем объем
тела, полученного вращением фигуры ОАВС, вычтем объем 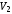 тела, полученного вращением фигуры ОАВ. Тогда искомый объем
тела, полученного вращением фигуры ОАВ. Тогда искомый объем 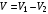 . По формуле
. По формуле 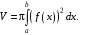 Найдем
Найдем 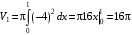 (ед. объема);
(ед. объема);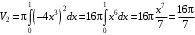 (ед. объема);
(ед. объема);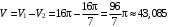 (ед. объема).
(ед. объема).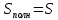
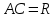
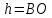 .
.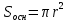
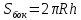
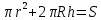
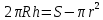
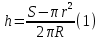
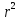 .
.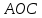 .Здесь
.Здесь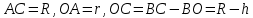
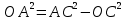
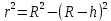
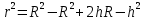
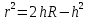
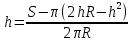
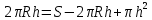
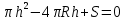
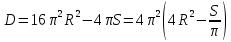
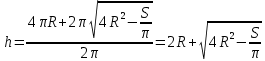
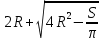 .
.