ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 3 из 32

ПРЕДЕЛЫ

Тема 1. Замечательные пределы

2.1. Числовая последовательность. Предел числовой последовательности, предел функции.

Определение. Числовой последовательностью называется функция натурального аргумента, то есть

x_n= f(n), n = 1, 2, 3, ....

Последовательность может обозначаться так: {x_n}, (x_n).

x_nназывается общим или n -ым членом последовательности. Последовательность считается заданной, если известна формула ее общего члена.

Например, 

Из школьного курса математики известны такие числовые последовательности, как арифметическая и геометрическая прогрессии. Формула n -ого члена арифметической прогрессии имеет вид a_n= a₁ + d(n – 1), где а₁ — первый член прогрессии, d — разность арифметической прогрессии; n -ый член геометрической прогрессии: b_n= b₁q^{n – 1}, где b₁ — первый член геометрической прогрессии, q — знаменатель геометрической прогрессии.

График числовой последовательности представляет собой не сплошную линию, а состоит из отдельных, изолированных точек (рис. 1.6).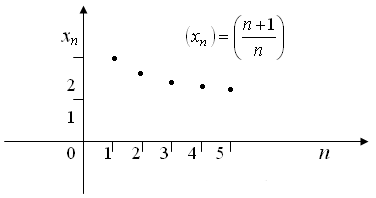



Рис. 1.6

Члены числовой последовательности можно изобразить точками на числовой прямой (рис. 1.7).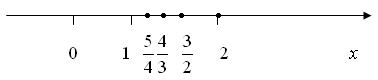



Рис. 1.7

Одной из основных операций математического анализа является операция предельного перехода. Если вернуться к числовой последовательности  , члены которой изображены на рисунках 1.6 и 1.7, то очевидно, что с ростом n члены последовательности скапливаются около 1, т.е. расстояния между членами последовательности   и 1 с увеличением n уменьшается. В этом случае говорят, что 1 есть предел числовой последовательности  .

Чтобы дать строгое определение понятия предела введем понятие   -окрестности точки а.

 -окрестностью точки а называется интервал (а –  ; а +  ) (рис. 1.8).



Рис. 1.8

Тот факт, что х принадлежит   -окрестности точки а означает, что выполняется неравенство |x – a| <   или а – e < x < а +  . Иначе это можно прочитать так: точка х находится от а на расстоянии меньшем чем  .

Говорят, что число а является пределом последовательности (x_n), если, начиная с некоторого номера, все ее члены попадают в сколь угодно малую 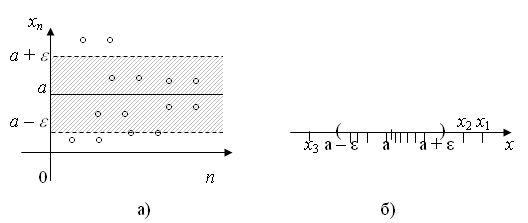  -окрестность точки а (рис. 1.9), а за пределами этой окрестности остается конечное число элементов последовательности. В этом заключается геометрический смысл предела числовой последовательности.



Рис. 1.9

Определение. Число а называется пределом последовательности (x_n), если для любого сколь угодно малого положительного числа   найдется такой номер N= N( ), зависящий от  , что для всех n> Nвыполняется неравенство

| x– a| < 

Это обозначается так:

Свойства пределов последовательностей

Так как числовая последовательность – это частный случай функции, то для неё также определены понятия монотонности, ограниченности.

1. Последовательность, имеющая предел ограничена.

2. Всякая ограниченная монотонная последовательность имеет предел.

3. Если последовательность имеет предел, то он единственный.

Последовательности, имеющие предел  , а ∈ R, называются сходящимися (к числу а), а последовательности, не имеющие конечного предела, – расходящимися.

Понятие предела числовой последовательности можно обобщить на произвольные функции.

Пусть функция y= f(x) определена в некоторой окрестности точки х₀, кроме, может быть, самой точки х₀.

Определение. Число у₀ называется пределом функции y= f(x) в точке х₀(или при стремлении х к х₀, х   х₀) если для любого числа   > 0 существует такое число   =  ( ) > 0, что для всех х, удовлетворяющих условию |x – x₀| <  , имеет место неравенство |f(x) – y₀| <  .

Обозначается: 

Геометрическая интерпретация данного определения такова, что для всех точек х, отстоящих от точки х₀ не далее чем на 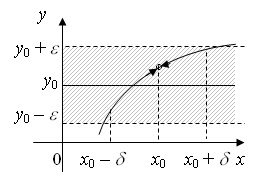 , точки графика функции y= f(x) лежат внутри полосы шириной 2 , ограниченной прямыми у = у₀ ±   (рис. 1.10).



Рис. 1.10

Определение. Число у₀ называется пределом функции y= f(x) при х    , если для любого числа  > 0 существует такое положительное число М, что для всех значений х, удовлетворяющих неравенству |х| > М, будет выполняться неравенство |f(x) – y₀| <  .

Обозначается: 

Геометрически это означает, что график функции y= f(x) будет находится в полосе, ограниченной прямыми у = у₀ ± 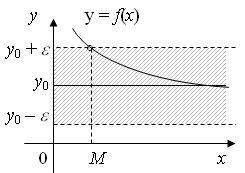 при любом |х| > М (рис. 1.11).



Рис. 1.11

Определение. Предел функции y= f(x) при х   х₀ называется бесконечным, если для любого положительного числа М существует число  > 0, такое, что для всех значений х, удовлетворяющих условию |х – х₀| <  , будет выполняться неравенство |f(x)| > M.

Обозначается  .

Геометрическая интерпретация данного определения представлена на рисунке 1.12.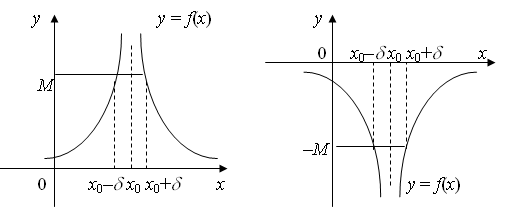



Рис. 1.12

Определение. Функция a = a (х) называется бесконечно малой функцией (или бесконечно малой, б.м.) при х   х₀, если

Аналогично определяются бесконечно малые при х    .

Бесконечно малые обозначают строчными буквами греческого алфавита  ,  , γ, ….

Определение. Функция y = f(x) называется бесконечно большой функцией (или бесконечно большой, б.б.) при х   х₀, если