ФУНКЦИИ. Тема Функции
 Скачать 1.59 Mb.
|
Тема 2. Предел функции нескольких переменных3. Число А называется пределом функции z = f (x, у) при х  х0, у у0, если для любого числа ε > 0 найдется число  > 0, зависящее от  , такое, что для всех точек (х, у), отстоящих от точки (х0, у0) не более, чем на , выполняется неравенство |f(х, у) – A| < .Цит. по: Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. — 2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. — (Серия «Золотой фонд российских учебников») — С. 390. 2.2. Непрерывность функции многих переменных Рассмотрим функцию двух переменныхn = 2; z = f(x,y). Возьмем точку (х0, y0) ∈ D(у)  R2. Дадим аргументу х в данной точке приращение  x, зафиксировав у0. Выражение x z = f(x0 + x, y0) - f(x0, y0)называется частным приращением функции по переменной х. Аналогично, фиксируя х0 и давая аргументу у приращение y, мы получим частное приращение по переменной у. y z = f(x0, y0 + y) - f(x0, y0).Выражение z = f (x0 + x, y0+ y) - f(x0, y0)называется полным приращением функции. Определение 11.6. Функция z = f(x, y) называется непрерывной в точке (x0, y0) ∈ D(у), если она определена в этой точке и малым приращениям аргументов соответствует малое полное приращение функции.  Определение 11.7. Функция z = f(x, y) называется непрерывной на множестве А D(z), если она непрерывна в каждой точке этого множества.Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 208–209. 15.4. Найти предел 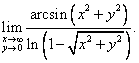 Решение Обозначим . Тогда условие x 0, y 0 равносильно тому, что r 0 и искомый предел примет вид: (применили правило Лопиталя. 15.5. Исследовать на непрерывность в точке (0; 0) функцию Решение Будем приближаться к точке (0; 0) по направлению прямых у = kх. Тогда будем иметь  Значения пределов различны при различных k,следовательно, предела функции двух переменных не существует, и функция не является непрерывной в точке (0; 0). Цит. по: Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. — 2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. — (Серия «Золотой фонд российских учебников») — С. 392. Если говорить точнее, то строго монотонными; к монотонным функциям, наряду с возрастающими и убывающими, относятся неубывающие и невозрастающие функции, т. е. такие, для которых при x1, x2 ∈ X, удовлетворяющих условию х2 > х1, соответственно f(x2) ≥ f(x1) или f(x2) ≤ f(x1). Под термином «период» подразумевается наименьший положительный период функции, равный 2  ; любой период функции у = sin x, как известно, равен 2 п, где п ∈ Z. |