ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 19 из 32

Тема 2. Механические и физические приложения интеграла

НЕКОТОРЫЕ МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Работа переменной силы F(x)
Путь, пройденный телом ((x) — скорость)
Статические моменты дуги плоской кривой (ρ(x) — плотность)
Моменты инерции дуги плоской кривой (ρ(x) — плотность)
Масса кривой (ρ(x) – плотность)
Координаты центра тяжести плоской кривой

Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 60.

Физические задачи.

Пример 107

Определить силу давления воды на стенку аквариума с основанием 1,8 м и высотой 0,6 м.

Дано: l = 1,8 м, h = 0,6 м, ρ =10³ кг/м³, g = 9,8 м/с²

Найти: F – ?

Решение:

Величина Р давления жидкости на горизонтальную площадку зависит от глубины ее погружения х, т.е. от расстояния площадки до поверхности жидкости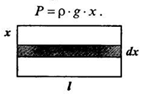



Площадь этой полоски ds = l   dx.

Пример 108

Через участок тела животного проходит или пульс тока, (мА). Длительность импульса 0,1с. Определить работу, совершаемую током за это время, если сопротивление участка 20 кОм.

Решение:

За малый интервал времени dt, на котором ток можно считать почти неизменным, совершается работа dA = J² Rdt. За время действия импульса совершенная работа равна

J = 20   10 ^–3e^5t A,

R = 20   10 ³ Ом,



Пример 109

Найти работу при растяжении мышцы на 4 см, если для ее растяжения на l см требуется нагрузка 10 H. Считать, что сила, необходимая для растяжения мышц пропорциональна ее удлинению.

Дано: L = 4 см = 0,04 м, x ₁ = 0,01 см, F₁ = 10 H

Найти: A – ?

Решение: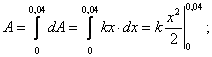



Найдем жесткость пружины:





Некоторые задачи экономики.

В экономических задачах переменная меняется дискретно, но достаточно часто. Для использования методов интегрирования, предполагающих непрерывность функций, надо составить модель (упрощенный аналог реального объекта), в которой аргументы и функции меняются непрерывно.

Пример 110

Найти количество произведенной продукции (дневную выработку) P за восьмичасовой рабочий день, если изменение производительности труда f(t) в течение дня можно описать формулой:

F ( t) = P₀(–0,2 t² + 1,6 t + 3),

где t — время в часах, P₀ — некоторая постоянная, имеющая размерность производительности.

Чему равен объем продукции P₃ за третий час рабочего дня?

Решение:

Эта формула вполне отражает реальный процесс работы (рис. 2.23). Производительность сначала растет, достигая максимума в середине рабочего дня при t — 4 ч, а затем падает.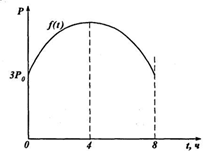



Рис. 2.23

Будем полагать, что производительность труда меняется в течение дня непрерывно, т.е. f(t) —непрерывная функция от времени t на отрезке [0,8].

Дневная выработка Р — это определенный интеграл — это площадь криволинейной трапеции, ограниченная сверху кривой f(t).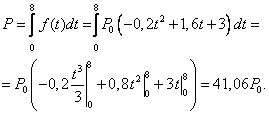



Объем продукции Р₃, произведенной за третий час рабочего дня равен:



Цит. по: Математика: учебное пособие /
В.П. Омельченко, Э. В. Курбатова. —
Ростов н / Д.: Феникс, 2007. — С. 154–157.