ФУНКЦИИ. Тема Функции
 Скачать 1.59 Mb.
|
Тема 2. Однородные дифференциальные уравнения первого порядкаДифференциальное уравнение первого порядка называется однородным, если оно может быть представлено в виде y' = g(y/x) для некоторой функции g. Уравнение y' = f(x, y) является однородным, если функция f(x, y) однородна степени ноль по переменным х, у, т.е. обладает свойством f(ax, ay) = f(x, y) для произвольного числа a . Замена переменной z = у/х, где z = z(x), сводит однородные дифференциальные уравнения к уравнениям с разделяющимися переменными. Уравнение вида  приводится к однородному в том случае, если прямые а1х + b1y + c1 = 0 и а2х + b2y + c2 = 0 пересекаются: достаточно перенести начало координат в точку пересечения этих прямых. В случае, если указанные прямые не пересекаются, то выражения (а1х + b1y) и (а2х + b2y) пропорциональны, и уравнение (12.12) решается с помощью замены переменной z = а1х + b1. 12.31. Решить уравнение  Решение. Правая часть уравнения (12.13) является однородной функцией степени 0 по переменным х и у, так как 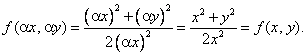 Поэтому само уравнение (12.13) — однородное. Для его решения воспользуемся заменой переменной z = у/х, где z = z(х). Тогда у' = zx, y' = z'x + z, и уравнение (12.13) принимает вид: или что равносильно т.е. приходим к уравнению с разделяющимися переменными. Выполняя почленное интегрирование последнего равенства, получаем Возвращаясь к исходной переменной, после преобразования имеем: 12 . 32. Решить уравнение  Решение. Поскольку  то правая часть уравнения (12.14) является функцией от выражения Прямые х + у = 0 и х + 1 = 0 пересекаются в точке (–1; 1), поэтому перейдем к новым переменным, выполняя параллельный перенос координатных осей в эту точку: t = x + 1, z = y – 1. Искомой функцией становится z = z(t). Так как то исходное уравнение принимает вид:  Для решения полученного однородного уравнения воспользуемся заменой переменной и = z/t, где и = и( t). Тогда z = ut, z' = u't + и и уравнение (12.15) принимает вид: u't = l + u2, или т.е. является уравнением с разделяющимися переменными. Выполняя почленное интегрирование последнего равенства, получаем arctg и = ln | t| + C, или и = tg ( ln |t| + C). Так как то (после преобразования) окончательно имеем y = 1 + (х + 1) tg(ln |x + 1| + C). Цит. по: Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. — 2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. — (Серия «Золотой фонд российских учебников») — С. 321–323. |