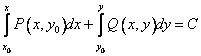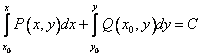ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 23 из 32

ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Тема 1. Линейные дифференциальные уравнения первого порядка

Линейное дифференциальное уравнение первого порядка имеет вид

a(x) y' + b(x) y + c(x) = 0, (6.2)

a(x)   0.

Разделим обе части уравнения на a (x).

y' + p(x) y + q(x) = 0, (6.3)

где p(x) =   q(x) = 

Будем искать решения уравнения (6.3) в виде произведения двух неизвестных функций:

y = u   v.

Подставим y = u   v в (6.3)



Выберем функцию u так, чтобы u' + p(x)u = 0: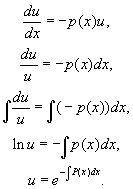



Подставим полученную функцию u(х) в (6.4) и найдем v(х):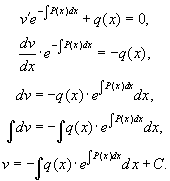



Подставим функции u(х) и v(х) в выражение для у:

 — общее решение линейного дифференциального уравнения первого порядка.

Пример 6.5. xy' - y - x - 1 = 0.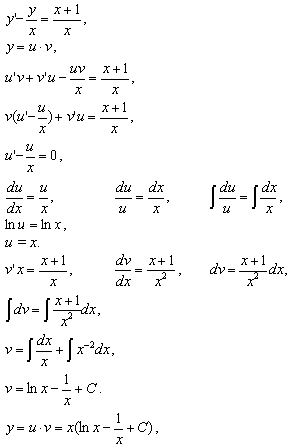



y = xln x+ Cx - 1 — общее решение уравнения.

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 99–101.

Дифференциальное уравнение первого порядка называется уравнением Бернулли, если оно имеет вид

y' + f(x) y = g(x)yⁿ,

где п   0, п   1.

Это уравнение приводится к линейному с помощью подстановки z = y^{1 – n} либо может быть непосредственно решено любым из двух описанных выше способов решения линейных уравнений.

12.45. Решить уравнение

Решение. Будем искать решение этого линейного уравнения в виде

у = и × v,

где v = v(x) — некоторое решение уравнения

u = u(x) —решение уравнения

vu' = x². (12.19)

Уравнение (12.18) — с разделяющимися переменными:

Выполняя почленное интегрирование последнего равенства, получаем:

ln |v| = – ln |x + 1| + C.

Поскольку в данном случае достаточно найти некоторое решение уравнения (12.18), то удобно полагать С = 0, тогда

Подставляя найденную функцию v в уравнение (12.19), приходим к уравнению

du = ( x³ + x²) dx.

В результате почленного интегрирования последнего равенства получаем

Таким образом, решение исходного уравнения имеет вид:

12.46. Решить уравнение

(у³ – ху)у' = 1.

Решение. Будем искать решение этого уравнения в виде x = х(у) (т.е. считая, что у — независимая переменная, а х — функция от у). Так как   то исходное уравнение линейно относительно функции х:

х' + ху = у³. (12.20)

Решим соответствующее однородное уравнение:

х' + ху = 0. (12.21)

Пусть х ≠ 0. Тогда

Последнее равенство равносильно

Учитывая, что х = 0 — решение уравнения (12.21), получаем, что общее решение этого уравнения имеет вид:

Полагая, что С₂ = С₂(у), найдем эту функцию из условия, что (12.22) — решение уравнения (12.20). Из (12.22) следует, что



Подставляя (12.22), (12.23) в (12.20), приходим к уравнению

или

Тогда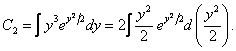



Применяя формулу интегрирования по частям, получаем:

Подставляя найденное выражение для функции С₂ = С₂(у) в (12.22), получаем решение уравнения (12.20):

12.47. Решить уравнение

Решение. Данное уравнение является уравнением Бернулли при n = 2. Отметим, что у = 0 является решением этого уравнения. Пусть у   0. Воспользуемся заменой переменной z = у^1 – n = у^–1. Тогда у = z^–1, у' = – z^–2 z' и исходное уравнение принимает вид:

Решим сначала однородное уравнение

Пусть z   0. Тогда

ln z| = ln |x| = lnC_2, (12.26)

где С₂ — произвольное положительное число. Равенство (12.26) перепишем в виде:

|z| = С₂ |х| или z = ± С₂ х.

Учитывая, что z = 0 является решением уравнения (12.25), получаем, что произвольное решение этого уравнения имеет вид:

z = С₁ х, (12.27)

где С₁ — любое число.

Положим теперь, что С₁ = С₁(х) и найдем эту функцию С₁ из условия, что (12.27) — решение уравнения (12.24). Из (12.27) следует, что

Тогда, учитывая (12.27), получаем, что уравнение (12.24) принимает вид:

или

dC₁ = dx,

и поэтому

С₁ = х + С.

Подставляя это выражение в (12.27), имеем решение уравнения (12.24):

z = ( x + C) x.

Так как   то окончательно решение исходного уравнения

имеет вид:

у (х² + Сх) = 1,

или

y = 0.

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 324–328.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Вид уравнения	Способ решения
Уравнения с разделяющимися переменными
y' = f(x)g(x)	Разделить переменные
M1(x)N1(x)dx + M2(y)N2(y)dy = 0
Однородные уравнения
	Использовать подстановку , y = t   x, y' = t'   x + t
б) P(x, y)dx + Q(x, y)dy = 0 где P(x, y), Q(x, y) — однородные функции одного порядка
в) y' = f(x, y), где f(x, y) — однородная функция нулевого порядка
Линейные уравнения
y' + p(x)y = f(x)	Использовать подстановку y = u   v, y = u'   v + v'   u (u, v — функции от x)
Уравнение Бернулли
y' + p(x)y = f(x)yn, где n   0, n   1.	Использовать подстановку y = u   v, y = u'   v + v'   u (u, v — функции от x)
Уравнение в полных дифференциалах
P(x, y)dx + Q(x, y)dy = 0 причем	Найти функцию, полный дифференциал которой стоит в левой части уравнения, по одной из формул