ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 24 из 32

Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 69.

Тема 2. Линейные дифференциальные уравнения с постоянными коэффициентами

Это уравнения вида: а₀y″ + a₁y′ + a₂y = 0, где a₀, a₁, a₂ — некоторые числа. Будем искать решение этого уравнения в виде y = e^kx. Разделим обе части уравнения на a₀   0.

y″ + py′ + q   y = 0,



Подставим в уравнение выражение для у: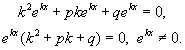



Следовательно, k² + pk + q = 0. Это уравнение называется характеристическим уравнением данного дифференциального уравнения. Найдем дискриминант этого уравнения

D = p² - 4q.

При этом возможны следующие случаи.

1. D > 0. Уравнение имеет два различных корня k₁, k₂. Общее решение имеет вид



2. D = 0. Уравнение имеет два одинаковых корня k₁ = k₂. Общее решение имеет вид



3. D < 0. Найдем два параметра a =   Общее решение имеет вид



Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 101–102.

ЛИНЕЙНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
Линейные однородные уравнения второго порядка с постоянными коэффициентами
ДУ: y'' + py' + qy = 0, где p , q ∈ R y''  k2 , y'  k , y  1 k2 + pk + q = 0 — характеристическое уравнение
Корни характеристического уравнения	Вид общего решения ДУ
Корни характеристического уравнения действительные, различные, т.е. k1   k2, (D > 0)
Корни характеристического уравнения действительные, равные, т.е. k1 = k2, (D > 0)
Корни характеристического уравнения комплексные, т.е. k1, 2 = a ± i (D > 0)

Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 70.

Пример 6.31. Решить уравнения: а) y'' – 3y' + 2y = 0; б) y'' – 2y' + y = 0; в) y'' – 2y' + 2y = 0.

Решение. а) Решая характеристическое уравнение λ² – 3λ + 2 = 0, находим его корни λ₁ = 1, λ₂ = 2. Тогда общее решение данного уравнения имеет вид y = C₁e^x+ C₂e^2x.

б) Решая характеристическое уравнение λ² – 2λ + 1 = 0, получаем λ₁ = λ₂ = 1. Согласно п. 2 теоремы общее решение дифференциального уравнения имеет вид y = (C₁ + C₂x)e^x.

в) Характеристическое уравнение λ² – 2λ + 2 = 0 не имеет действительных корней. В этом случае согласно п. 3 теоремы общее решение дифференциального уравнения имеет вид

y = C₁e^xsin x + C₂e^xcos x ( a =   = 1).

Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 241.