ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 27 из 32

Тема 2. Знакопеременные ряды

2.1. Знакопеременные ряды

Числовой ряд, члены которого имеют различные знаки, называется знакопеременным рядом.

Пусть дан знакопеременный ряд

. (7.1)

Рассмотрим ряд, составленный из модулей его членов:



Определение 7.4. Ряд (7.1) называется условно сходящимся, если сам ряд (7.1) сходится, а ряд (7.2), составленный из абсолютных величин, расходится.

Определение 7.5.Ряд (7.1) называется абсолютно сходящимся, если сам ряд (7.1) сходится и ряд из абсолютных величин тоже сходится.

Пример 7.7.   — ряд сходится,

 — ряд расходится.

Таким образом, ряд является условно сходящимся.

Пример 7.8.   — ряд сходится,

 — ряд сходится.

Ряд является абсолютно сходящимся.

Теорема 7.7.Если ряд, составленный из абсолютных величин членов знакопеременного ряда, сходится, то и сам ряд сходится (из абсолютной сходимости следует условная).

2.2 Знакочередующиеся ряды

Знакопеременный ряд, у которого соседние члены имеют противоположные знаки, называется знакочередующимся. Общий вид знакочередующегося ряда:



Теорема 7.8.(достаточный признак Лейбница сходимости знакочередующегося ряда). Если абсолютные величины членов знакочередующегося ряда   монотонно убывают, т. е.   и предел n -го члена с ростом n стремится к нулю   то ряд сходится.

Пример 7.9.  следовательно, ряд сходится.

Пример 7.10.   следовательно, ряд сходится.

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 110–111.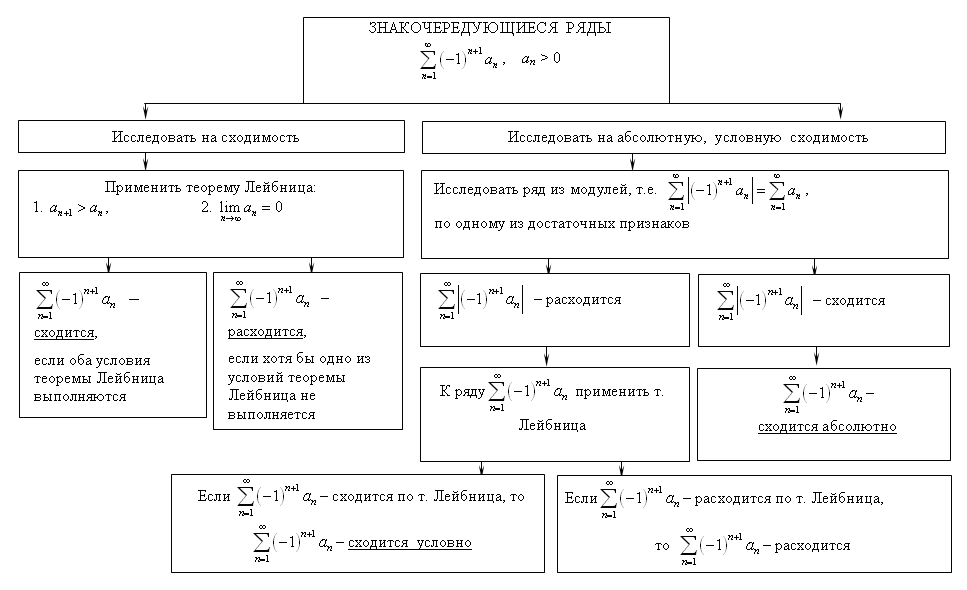



Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 74.

13.68. Выяснить, какие из данных рядов являются сходящимися, а какие — расходящимися. Для сходящихся рядов определить, сходятся они абсолютно или условно.



Решение

а) В данном случае. При п   3 члены данного знакочередующегося ряда убывают по абсолютной величине,   Отбрасывание конечного числа членов ряда не влияет на его сходимость, поэтому по признаку Лейбница ряд сходится.

Определим тип сходимости ряда. Для этого исследуем сходимость ряда, составленного из модулей членов данного ряда. Его члены равны   Применим предельный признак сравнения., в качестве эталонного ряда возьмем гармонический ряд, v_n = 1/ n. Имеем   т.е. предел k конечен и отличен от нуля, и исследуемый ряд ведет себя так же, как и эталонный ряд. Из расходимости эталонного ряда следует расходимость исследуемого ряда.

Таким образом, сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, т.е. ряд сходится условно.

б) Члены этого ряда имеют разные знаки, поэтому найдем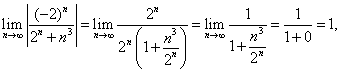



ибо   (это можно проверить трехкратным применением правила Лопиталя). Предел модуля общего члена ряда отличен от нуля, поэтому ряд расходится.

в) Члены данного ряда убывают по абсолютной величине и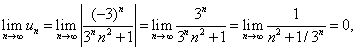

 ибо при n     n 2    , а 1/3n   0. Следовательно, по признаку Лейбница ряд сходится.

Исследуем сходимость ряда, составленного из модулей членов данного ряда. Его члены имеют вид   Применим предельный признак сравнения. В качестве эталонного ряда возьмем сходящийся ряд с членами v_n = 1/ n2.Имеем 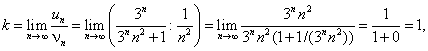  предел k конечен и отличен от нуля, следовательно, исследуемый ряд ведет себя так же, как и эталонный ряд, т.е. сходится.

Таким образом, сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов, т.е. ряд сходится абсолютно.

13.69. Найти сумму ряда   с точностью до 0,0001.

Решение

У данного ряда   его члены удовлетворяют условиям признака Лейбница, поэтому ряд сходится. Для того чтобы определить количество членов, подлежащих суммированию для вычисления суммы ряда с заданной точностью, будем выписывать члены ряда до тех пор, пока не найдем член, по модулю меньший, чем 0,0001 = 1/10000: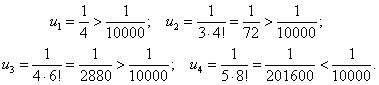



Таким образом, для достижения требуемой точности достаточно вычислить S₃:|S – S₃| < u₄ < 0,0001, т.е. достаточно взять три первых члена ряда:



Результат должен быть получен с точностью до 0,0001, поэтому окончательный ответ не может содержать более 4 цифр после запятой. При последнем округлении была допущена дополнительная ошибка, не превосходящая 0,00005. Итоговая ошибка при вычислении суммы ряда не больше 0,00005 + u₄   0,00005 + 1/201600   0,000055 < 0,0001.

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 358–360.