ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 25 из 32

Тема 3. Линейные неоднородные дифференциальные уравнения

Пусть дано дифференциальное уравнение



и соответствующее ему однородное уравнение



Теорема 6.1.Общее решение неоднородного уравнения (6.5) можно представить в виде суммы общего решения однородного уравнения (6.6) и любого частного решения неоднородного уравнения (6.5).

Доказательство.

Пусть   — общее решение однородного уравнения (6.6). Так как это уравнение второго порядка, то это решение зависит от двух произвольных постоянных. Пусть   — какое-либо частное решение неоднородного уравнения (6.5). Покажем, что их сумма   является общим решением неоднородного уравнения (6.5).

Функция y зависит от двух произвольных констант. Подставим y в (6.5).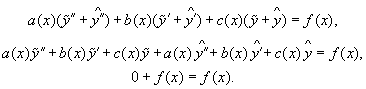



Таким образом, у является решением неоднородного уравнения (6.5) и так как оно зависит от двух произвольных постоянных, то у является общим решением неоднородного уравнения (6.5).

Для того чтобы найти общее решение неоднородного уравнения, надо найти общее решение соответствующего однородного и какое-либо частное решение неоднородного уравнения.

Для уравнения с постоянными коэффициентами частное решение неоднородного уравнения подбирается по виду правой части f(x):

1) если f(x) — многочлен, то частное решение ищут в виде многочлена той же степени с неизвестными коэффициентами;

2) если f(x) зависит от синуса и косинуса одного аргумента, то частное решение ищут в виде суммы синуса и косинуса этого же аргумента с неизвестными коэффициентами;

3) если в правой части — показательная функция, умноженная на многочлен, то частное решение ищут в виде произведения многочлена той же степени с неизвестными коэффициентами, умноженного на показательную функцию с тем же аргументом, что и в уравнении.

Пример 6.6.   — неоднородное уравнение.

 — соответствующее ему однородное уравнение.



 — общее решение однородного уравнения.

Будем искать частное решение неоднородного уравнения в виде



Подставим эту функцию в неоднородное уравнение: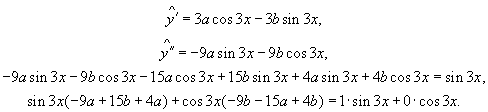



Приравняем коэффициенты при sinx и cosx.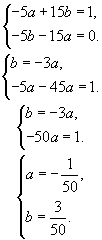



 — частное решение неоднородного уравнения.

 — общее решение неоднородного уравнения.

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 102–104.

ЛИНЕЙНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
Линейные неоднородные уравнения с постоянными коэффициентами и специальной правой частью
ДУ: y'' + py' + qy = Pn(x)e x k2 + pk + q = 0 — характеристическое уравнение Общее решение:
Корни характеристического уравнения	Вид частного решения	Вид многочлен
1.   — не корень характеристического уравнения, т.е.    k1,     k2		n = 0 Q0(x) = A, n = 1 Q1(x) = Ax + B, n = 2 Q2(x) = Ax2 + Bx + C, n = 3 Q3(x) = Ax3 + Bx2 + Cx + D
2.   — однократный корень характеристического уравнения, т.е.  = k1 или   = k2
3.   — двукратный корень характеристического уравнения, т.е.  = k1 = k2
Линейные неоднородные уравнения с постоянными коэффициентами и специальной правой частью
ДУ: y'' + py' + qy = M cos  x + N sin  x k2 + pk + q = 0 — характеристическое уравнение Общее решение:
Корни характеристического уравнения			Вид частного решения
±  i — не корень характеристического уравнения ±  i   k1, 2
±  i — корень характеристического уравнения ±  i = k1, 2

Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 71.

Примеры: 1) у" + у' = 5х + 3. Ищем решение в виде  .

а) y* — общее решение уравнения у" + у' = 0, его характеристическое уравнение k² + k = 0, т.е. k₁ = 0, k₂ = –1   у* = с₁ + c₂e^–x:

б)   — частное решение уравнения у" + у' = 5х + 3 — ищем в виде   так как правая часть уравнения — многочлен первой степени и k₁ = 0. Подставим   в уравнение:



2A + B = 3   A = 5/2, B = –2.

Таким образом, y = c₁ + с₂е^– x + 5х²/2 – 2х

2) y '' – 2у' – 3у = (х + 2)е^3 x

Ищем обшее решение в виде.

а) у* — общее решение уравнения у" – 2у' – 3у = 0. его характеристическое уравнение k² – 2 k – 3 = 0, т.е. k₁ = –1, k₂ = 3 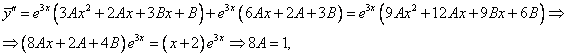  у* = с₁e^–x + c₂е^3x:

б) 





2A + 4B = 2   A = 1/8, B = 7/16.

3) y" + 4у' + 5у = 2cos x – sin x /

Ищем решение в виде.

а) у* — общее решение уравнения у" + 4у' + 5у = 0, его характеристическое уравнение k² + 4 k + 5 = 0, т.е. k_{1, 2} = – 2 ± i 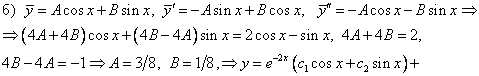  у* = e^–x (с₁ cos x + c₂ sin x );



Цит. по: Математика: учебное пособие / Ю.М. Данилов,
Л.Н. Журбенко, Г.А. Никонова, Н.В. Никонова, С.Н. Нуриева;
под ред. Л.Н. Журбенко, Г.А. Никоновой. —
М.: ИНФРА-М, 2006. — С. 257–258.