ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 28 из 32

Тема 3. Функциональные ряды. Область сходимости. степенные ряды

Определение 7.6. Ряд вида f1(x) + f2(x) + f3(x) + …+ fn(x) + … =   называется функциональным рядом. При x = x0 данный ряд превращается в числовой ряд , который можно исследовать на сходимость.

Определение 7.7.Множество действительных чисел А называется областью сходимости функционального ряда, если для любых x ∈ A соответствующий числовой ряд сходится.

Функциональный ряд является функцией, определенной на области сходимости.

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 112.

Рассматриваются степенные ряды вида

с₀ + с₁х + с₂х2 + ... + с_пхп +..., (105)

членами которых являются степенные функции, где числа с₀, c₁,..., c_n — коэффициенты степенного ряда.

Совокупность тех значений х, при которых степенной ряд (105) сходится, называется областью сходимости степенного ряда.

Пример 6.46. Найти область сходимости степенного ряда

1 + x + x2 +... + xn +...

Решение.

Данный ряд можно рассматривать как геометрический ряд со знаменателем q = x, который сходится при |q| = |х| < 1. Отсюда –1 < х < 1, т.е. областью сходимости является интервал (–1; 1).

Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.

Теорема Абеля. 1.Если степенной ряд сходится при значении х = х ₀   0 (отличном от нуля), то он сходится и притом абсолютно при всех значениях х таких, что |х| < |х₀|. 2. Если степенной ряд расходится при х = х₁, то он расходится при всех значениях х таких, что |х| > |х₁|.

Из теоремы Абеля (рис. 6.27) следует, что существует такое число R 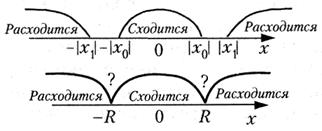  0,что при |х| < R , или х ∈ (–R; R), ряд сходится, а при |х| < R — расходится.



Рис. 6.27

Число R называется радиусом сходимости, а интервал (–R; R) — интервалом сходимости степенного ряда.

На концах интервала сходимости, т.е. при х = –R и х = R, ряд может как сходиться, так и расходиться (см. рис. 6.27).

Радиус сходимости ряда при условии, что в нем все коэффициенты с_п, по крайней мере начиная с некоторого номера п, отличны от нуля, определяется по формуле

или по формуле

Для некоторых рядов интервал сходимости вырождается в точку (R = 0), для других охватывает всю ось Ox (R =  ).

Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 261–262.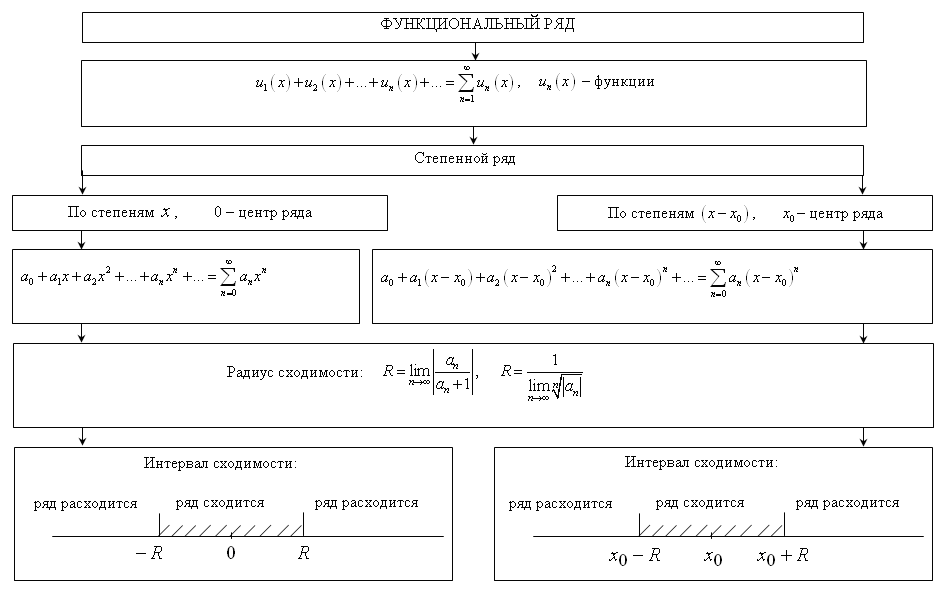



Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 75.

Пример 6.47. Найти область сходимости степенного ряда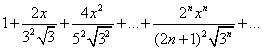



Решение.

Найдем радиус сходимости ряда: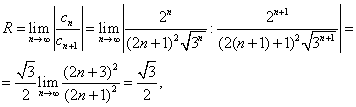



т.е. интервал сходимости ряда 

Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при   данный степенной ряд принимает вид   этот ряд сходится по признаку Лейбница. На правом конце при   получаем ряд   представляющий обобщенный гармонический ряд при   = 2, у которого все члены с четными номерами равны нулю. Так как   = 2 > 1, то этот ряд сходится.

Следует отметить, что сходимость ряда на левом конце интервала сходимости при   могла быть установлена с помощью достаточного признака сходимости знакопеременного ряда, так как ряд, составленный из абсолютных величин его членов, т.е. ряд   сходится.

Итак, область сходимости данного ряда 

Свойства степенных рядов. Пусть функция f(x) является суммой степенного ряда, т.е.   Степенные ряды по своим свойствам напоминают конечные суммы (многочлены): на любом отрезке [а, b], целиком принадлежащем интервалу сходимости (–R; R), функция f(x) является непрерывной, а следовательно, степенной ряд можно почленно интегрировать на этом отрезке:



Кроме того, в интервале сходимости степенной ряд можно почленно дифференцировать:

При этом после интегрирования или дифференцирования полученные ряды имеют тот же радиус сходимости R.

Функция f(x), определенная и п раз дифференцируемая в окрестности точки х = 0, может быть представлена в виде суммы степенного ряда или, иными словами, может быть разложена в степенной ряд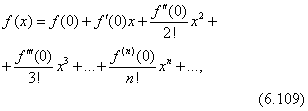



называемый рядом Маклорена.

Следует отметить, что только многократной дифференцируемости функции f(x) может оказаться недостаточной для ее разложения в ряд Маклорена, ибо последний может расходиться, либо сходиться — но не к функции f(x).

Для того чтобы ряд Маклорена сходился к функции f(x), необходимо и достаточно, чтобы при п     остаток ряда стремился к нулю, т.е.

для всех значений х из интервала сходимости ряда.

Достаточным условием разложения функции f(x) в ряд Маклорена является ограниченность всех ее производных в окрестности точки х = 0 одним и тем же числом, т.е. |f(n)(x)| ≤ C(n = 1, 2, 3, …).

Если функция f(x) может быть разложена в ряд Маклорена, то это разложение единственное.

Наряду с рядом Маклорена в теории рядов рассматривается ряд Тейлора: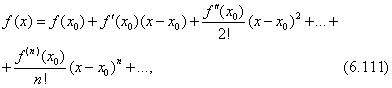



представляющий разложение данной функции по степням (х – х₀). Ряд Маклорена (109) является частным случаем ряда Тейлора (111) при х₀ = 0.

Ряд Тейлора тесно связан с формулой Тейлора: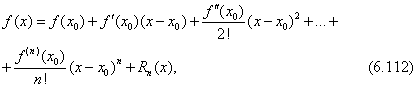



где R_n(x) — остаточный член формулы Тейлора:



 ∈ (x₀; x) (или   ∈ (x; x₀)), записанный в форме Лагранжа.

Очевидно, что при выполнении условия (110) остаток r_n(х) ряда Тейлора равен остаточному члену R_n(x) формулы Тейлора.

Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 262–265.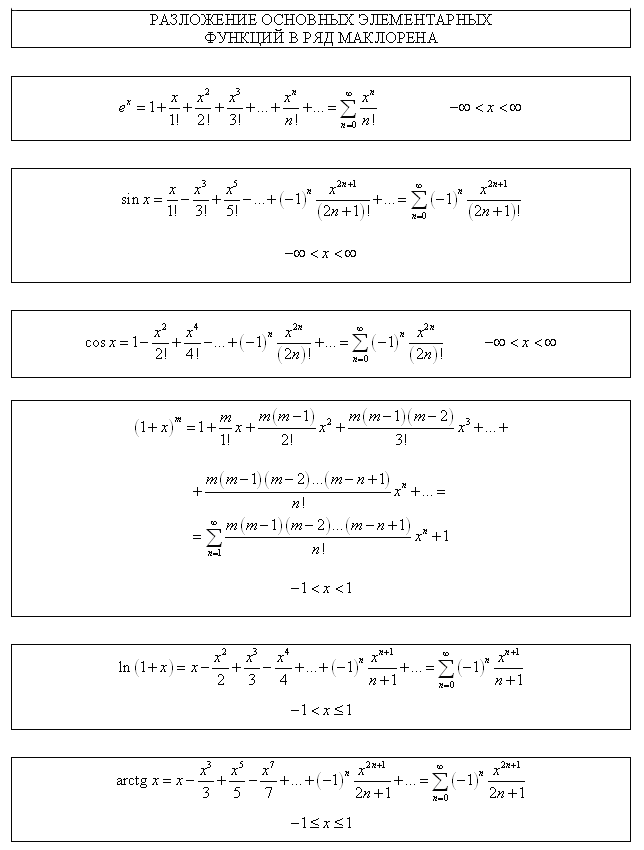





Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 76, 77.

Существует несколько способов разложения функций в степенной ряд. Проиллюстрируем их на конкретных примерах.