ФУНКЦИИ. Тема Функции
 Скачать 1.59 Mb.
|
Применение правила умножения рядов14.26. Разложить в ряд по степеням х функцию y = ехln(1 + х). Решение В интервале (–1; 1) имеют место разложения. По правилу умножения рядов получим: 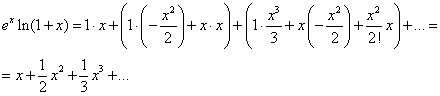 Область сходимости ряда (–1; 1). Применение почленного интегрирования14.27. Разложить в ряд по степеням х функцию у = arcsin х. Решение Среди готовых разложений ряда для данной функции нет. В то же время производная этой функции может быть разложена в степенной ряд с помощью биномиального ряда:  Учитывая, что искомый ряд найдем почленным интегрированием данного ряда на отрезке [0; х], принадлежащем интервалу сходимости ряда (–1; 1):  14.28. Разложить в ряд по степеням x: функцию у = cos 2x, применяя различные способы. Решение: Первый способ. Применим метод непосредственного разложения. Вначале найдем производные до n -го порядка и вычислим их значения при х = 0: f(x) = cos2x; f'(x) = –2cosx sinx = –sin2x; f"(x) = –2cos2x; f'"(x) = 22sin2x ; f(4)(x) =23cos2x; f(5)(x) = –24sin2x и т. д. Теперь запишем ряд:  или  Область сходимости ряда, как нетрудно убедиться, есть (–  ; + ).Второй способ. Учитывая, что используем готовое разложение в ряд функции cosx (в котором вместо х берем 2х), умножаем обе части полученного равенства на а затем прибавляем к ним 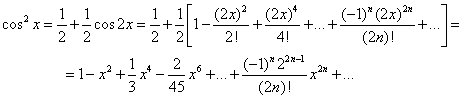 Третий способ. Для функции f(x) = cosx, имеющей разложение, т.е.  применим правило возведения в квадрат степенного ряда: 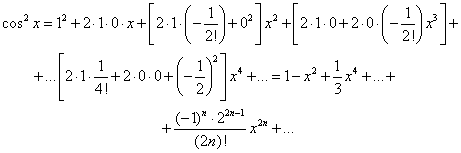 Четвертый способ. Относительно легко можно разложить в ряд производную функции f(x) = cos 2x , т.е. f'(х) = –2cosx sinx = –sin 2x (берем члены ряда с противоположными знаками, а вместо х берем 2х): Для получения искомого разложения почленно интегрируем полученный ряд на отрезке [0; х], принадлежащем интервалу сходимости (– 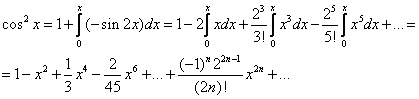; + ), т.е. при любом х: (к полученному почленным интегрированием ряду добавили 1, так как  14.58. Вычислить приближенно с точностью до 0,0001:  Решение а) Для вычисления запишем ряд при х = –3/4, принадлежащем области сходимости (– 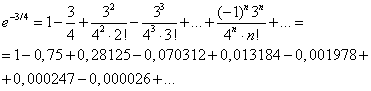; + ): Взяв первые семь членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда мы допустим погрешность |rn|, не превышающую первого отброшенного члена (по абсолютной величине), т.е. |rn| ≤0,000026 < 0,0001. Итак, складывая первые семь членов, получим Более точно оценить погрешность вычисления можно, используя формулу Тейлора.Взяв в качестве величины еx первые (n + 1) членов ряда (вместе с нулевым), мы допускаем погрешность, определяемую остаточным членом Rnпри х 0 = 0, 0 <  < х или х < < 0:Для функции  Следовательно, при х = –3/4  При n = 6, т.е. просуммировав вместе с нулевым 7 членов ряда, мы получим при этом остаточный член заключен в границах от минимального до максимального т.е. –0,000026 < Rn < –0,000013. Следовательно, точное значение находится в пределах от 0,472365 до 0,472378. Неизменны 4 десятичных знака, следовательно, с точностью до δ = (Легко показать, что суммирование менее, чем семь членов ряда (n < 6), не обеспечивает данной в условии точности ответа.) б) Для вычисления ln 0,6 запишем ряд при х = –0,4, входящем в область сходимости ряда (–1; 1]: 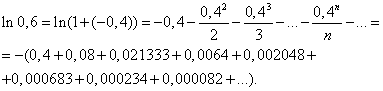 Если в качестве ln 0,6 взять первые восемь членов, мы допустим погрешность 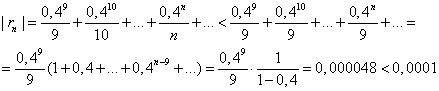 (мы учли, что сумма сходящегося геометрического ряда в скобках равна). Итак, складывая первые восемь членов, получим: ln 0,6  –0,510780 –0,5108.Заметим, что при суммировании только семи членов погрешность  т.е. не удовлетворяет заданной в условии точности до 0,0001.Замечание. Оценка погрешности вычисления ln 0,6 с помощью остаточного члена формулы Тейлора оказывается в данном случае менее эффективной. Действительно,для функции f(х) = ln(1 + х) тогда по формуле остаточный член 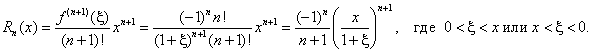 При n = 8, х = –0,4 Следовательно, Rn(–0,4) < Rn< Rn(0), или –0,002890 < Rn < –0,000029, а значит, –0,510780 – 0,002890 < ln 0,6 < –0,510780 – 0,000029, т.е. –0,513670 < ln 0,6 < –0,510809, что гарантирует точность вычисления лишь до 0,01 (а точнее, до 0,003). в) Вычислить ln 3 = ln(1 + 2) с помощью ряда для функции у = ln (1 + x) не представляется возможным, так как х = 2не входит в область сходимости ряда (–1; 1]. Воспользуемся рядом: 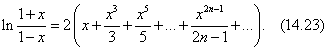 Этот ряд позволяет вычислять логарифмы любых чисел, так как при изменении х в интервале сходимости ряда (–1; 1) дробь меняется в интервале (0; + ).Пусть |