ФУНКЦИИ. Тема Функции
 Скачать 1.59 Mb.
|
Тема 3. Дифференциальные уравнения высших порядков3.1. Основные понятия об ОДУ 2-го порядка ОДУ 2-го порядка в общем виде записывают так: F(x, у, у', у") = 0. (21.1) Если уравнение (21.1) можно разрешить относительно у", то оно имеет вид у" = f(x, у, у') (21.2) Определение: Задача нахождения решения уравнения (21.2), удовлетворяющего начальным yсловиям y(x0) = y0, y'(x0) = y0' называется задачей Коши. Теорема. (существования и единственности решения ОДУ 2-го порядка): Если f(x, у, у') и ее частные производные непрерывны в окрестности т. в пространстве переменных (х, у, у'), то в окрестности т. х0 существует единственное решение задачи Коши: Теорему приводим без доказательства. Определение: Общим решением дифференциального уравнения (21.2) называется функция у =  (x, с1, c2), зависящая от двух произвольных постоянных с1, c2 при следующих условиях:1) она является решением (21.2) при любых значениях с1, c2; 2) при любых начальных условиях существуют единственные значения c1 = c10, c2 = c20, что у = (x, с10, c20) удовлетворяет данным начальным условиям, т. (x1, x0, y'0) ∈ D - ! решения.Условия, которые используются для нахождения постоянных с10, c20 в общем решении ОДУ 2-го порядка, можно задать по другому. Пусть, например, решение уравнения ищется на отрезке x ∈ [ a; b]. Тогда для определения с10 и c20 можно задать т.е. задачу для ОДУ 2-го порядка можно сформулировать следующим образом: на отрезке [ a; b] найти решение ОДУ 2-го порядка, удовлетворяющее условиям, заданным на концах отрезка: F(x, у, у', у") = 0, y(a) =ya, y(b) = yb. Такая задача называется краевой задачей для ОДУ 2-го порядка. 3.2. ДУ 2-го порядка, допускающие понижение порядка Определение: ДУ 2-го порядка, допускающими понижение порядка, называются уравнения, решение которых можно путем замены переменных свести к решению уравнений 1-го порядка. К ним относятся: а) у" = f(x, y'), б)у" = f(y, y'). (Уравнения вида у" = f(х) являются частным случаем уравнения у" = f(x, y'). Они в явном виде не содержат переменной у в случае а) и x в случае б), поэтому в случае а) делают замену y' = p, p = p(x), y'' = p, а в случае б) y' = p, p = p(y), Примеры: 1) (1 + x2) y" – 2ху' = 0. Замена y' = p, p = p ( x), y'' = p'  (1 + х2)p' – 2хр = 0 — уравнение с разделяющимися переменными  y' = c1(1 + x2) dy = c1(1 + x2)dx y = c1 (x + x3/3) + c2.2) 1 + y'2 –= 2 yу''. Замена y' = p, p = p(y), у" = р'р, 1 + р2 = 2урр' — уравнение с разделяющимися переменными 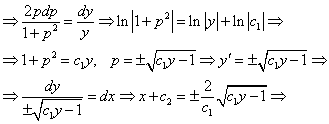  Цит. по: Математика: учебное пособие / Ю.М. Данилов, Л.Н. Журбенко, Г.А. Никонова, Н.В. Никонова, С.Н. Нуриева; под ред. Л.Н. Журбенко, Г.А. Никоновой. — М.: ИНФРА-М, 2006. — С. 251–253.
Цит. по: Высшая математика в схемах и таблицах / Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 70. 12.60. Решить уравнение y" = y' ctg x. Решение. Положим z = 1. Тогда у" = (у')' = z' и исходное уравнение принимает вид z' = z ctg x. (12.28) Пусть z  0. Тогда из (12.28) следует:или Интегрируя почленно последнее равенство, получаем ln |z| = ln |sin x| + lnC1, где С1 > 0, или z = ± С1 sin x. Так как z = 0 является решением уравнения (12.28), то произвольное решение этого уравнения имеет вид: z = С1 sin x, (12.29) где С1 — произвольное число. Так как то из (12.29) следует: dy = С1 sin xdx. Интегрируя последнее равенство, окончательно получаем у = –С1 cos x + C2. 12.61. Решить уравнение yy" = y2y' + ( y')2, Решение. Пусть z = y', тогда , где и исходное уравнение принимает вид: dy yzz' = y2 z + z, (12.30) т.е. становится уравнением относительно функции z = z(y). Очевидно, z = 0 — решение уравнения (12.30), откуда у = С, где С — произвольное число. Пусть z 0. Тогда из (12.30) следует, чтоyz' = y2 + z (12.31) — линейное уравнение первого порядка. Решение этого уравнения будем искать в виде z = uv, где v = v(y) — некоторое решение уравнения yv' – v = 0, (12.32) и = и (у) — решение уравнения u' v = y. (12.33) Решая (12.32), в частности, имеем v = у. Тогда (12.33) приводит к уравнению и' = 1, откуда и = у + С1, т.е. решение (12.31) имеет вид: z = y2 + C1 y. Так как z = y', то приходим к уравнению Пусть С1 = 0. Тогда при y 0 имееми, следовательно, х – у–1 + С2, или у = (С2 – х)–1. (12.34) Пусть C1 0, тогда и после интегрирования: 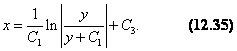 Окончательно решение исходного уравнения имеет вид у = С или (12.34), или (12.35) Цит. по: Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. — 2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. — (Серия «Золотой фонд российских учебников») — С. 329–330. | |||||||||||||||||||||
(x + 7) = y'