однородные тригонометрические уравнения. Жумакожиева экзамен профф.русский н. Однородные тригонометрические уравнения и сводящиеся к ним
 Скачать 252.43 Kb. Скачать 252.43 Kb.
|
|
Западно-Казахстанский Университет им. М. Утемисова  Физико-математический факультет Реферат По предмету «Профессиональный русский язык» На тему: «Однородные тригонометрические уравнения и сводящиеся к ним». Выполнила студ. группы М-31: Жумакожиева А.А. Проверила: Лукпанова Л.Х. 2020-2021 Содержание Введение…………………………………………………………………….….3 Теоретический раздел Глоссарий по теме………………………………………………………4 Однородные уравнения ………………….……………………………..5 Однородные тригонометрические уравнения первой и второй степени…...................................................................................................6 Раздел решения задач Решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки………………………………..……7 Решение более сложных тригонометрических уравнений…….........11 Заключение …………………………………………………………………...14 Список литературы…………………………………………………...………15 Введение Тригонометрия возникла как аппарат для вычисления неизвестных параметров треугольника по заданным значениям других его параметров. Так, методами тригонометрии по данным сторонам треугольника можно вычислить его углы, по известной площади и двум углам вычислить стороны и т.д. Необходимость отыскивать неизвестные параметры данного треугольника впервые возникла в астрономии, и в течение долгого времени тригонометрия была одним из ее разделов. Первые методы нахождения неизвестных параметров данного треугольника были развиты учеными Древней Греции за несколько веков до нашей эры. Греческие астрономы не рассматривали синусов, косинусов и тангенсов. Вместо таблиц этих величин они составили и использовали таблицы, позволяющие отыскивать хорду окружности по стягиваемой ею дуге. Дальнейшее развитие тригонометрия получила в средние века в работах индийских и арабских ученых. Современные буквенные обозначения появились в тригонометрии в середине XVIII века. Приблизительно в то же время в тригонометрии стала рассматриваться радианная мера угла, были введены тригонометрические и обратные тригонометрические функции числового аргумента, после чего тригонометрия приобрела свой современный вид. Глоссарий по теме Синус угла 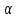 – ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол – ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол 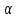 . .Обозначается 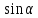 . .Косинус угла 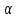 – абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол – абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол 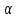 . .Обозначается 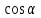 . .Тангенс угла 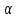 – отношение синуса угла к его косинусу. – отношение синуса угла к его косинусу.Обозначается 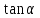 . .Котангенс угла 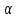 отношение косинуса угла к его синусу. отношение косинуса угла к его синусу.Обозначается 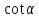 . .Арккосинусом числа Арксинусом числа Арктангенсом числа m называется такое число α, что: Арккотангенсом числа n называется такое число α, что: Уравнение вида: называется однородным. Здесь f и g произвольные функции, 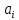 - коэффициенты. - коэффициенты.Универсальная тригонометрическая подстановка - это формулы для выражения синуса, косинуса и тангенса аргумента через тангенс половинного аргумента: 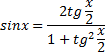 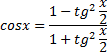 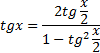 Все тригонометрические функции рационально выражаются через sinx и cosx, то в общем случае рациональное уравнение относительно тригонометрических функций одного аргумента можно представить в виде Где R – рациональная функция относительно sinx и cosx. Если 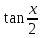 с помощью формул, выражающих тригонометрические функции через тангенс половинного аргумента. Однако, решая уравнение таким методом, можно потерять корни вида с помощью формул, выражающих тригонометрические функции через тангенс половинного аргумента. Однако, решая уравнение таким методом, можно потерять корни вида 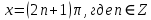 для которых для которых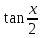 не имеет смысла. Поэтому необходимо проверять, являются ли числа не имеет смысла. Поэтому необходимо проверять, являются ли числакорнями исходного уравнения. Если уравнение вида (1) или приводимое к нему при замене Если уравнение (1) или приводимое к нему не изменяется при замене Если уравнение (1) или приводимое к нему при замене не изменяется, то его имеет смысл приводить к рациональному относительно tgx. Однородные уравнения Однородные тригонометрические уравнения имеют такой вид: a sin2x + b sinxcosx + c cos2x = 0 (однородное уравнение 2-й степени) или a sin3x + b sin2x cosx + c sinx cos2x + d sin3x = 0 (однородное уравнение 3-й степени) и т.д. Общий вид однородного тригонометрического уравнения: В этих уравнениях sinx ¹ 0, cosx ¹ 0. Решаются они делением обеих частей уравнения на sinnx или на cosnx и приводятся к уравнениям относительно tgx или ctgx: или Справедливы соотношения: tg a ctg a=1 tg a=1/ctg a ctg a=1/tg a 1+tg2a=1/cos2a 1+ctg2a=1/sin2a Уравнение вида atg x+bctgx+c=0 приводится к квадратному уравнению одной тригонометрической функции путем замены ctgx=1/tgx Уравнение вида Уравнение вида Называется однородным уравнением второй степени относительно sin f(x) и cosf(x) если все три коэффициента a, b, k или какие-либо два из них отличны от нуля. Считая, что Уравнение (2) равносильно уравнению (1), т.к. корни уравнения cos2f(x)=0 не являются корнями уравнения (1). Однако если a=0, то уравнение (1) принимает вид Как, например, быть в том случае, когда тригонометрическое уравнение выглядит, например, так: Для этого нам нужно рассмотреть некоторые вспомогательные приемы решения уравнений, а также формулы преобразования тригонометрических выражений. 1. Итак, рассмотрим однородное тригонометрическое уравнение. Напомним определение однородного уравнения Определение Уравнение вида: Здесь f и g произвольные функции, В зависимости от значения показателя n, мы можем получить однородное уравнение первой, второй или более высокой степени. Например, уравнение 2. Теперь перейдем к рассмотрению однородных тригонометрических уравнений. Если функции f и g это синус и косинус одного и того же аргумента, то мы получим тригонометрическое однородное уравнение. Рассмотрим сначала однородное тригонометрическое уравнение первой степени. Запишем его в общем виде: Разделим это уравнение на Решать такие уравнения мы умеем: Заметим, что, решая это уравнение, мы выполняли деление уравнения на выражение с переменной. Так как это действие не является равносильным, проверим, не потеряли ли мы корни. Если Пример 1. Решить уравнение: Решение: Ответ: Решим теперь однородное тригонометрическое уравнение второй степени Общий вид такого уравнения: Так же, как и уравнение (1), разделим его на наибольшую степень косинуса х. Так же, как и при решении уравнения (1), мы должны убедиться в том, что при делении уравнения на выражение с переменной мы не потеряли корней. Это не произойдет в том случае, если После деления мы получили квадратное уравнение относительно тангенса х, которое и решаем известными способами. При решении этого уравнения мы можем вводить новую переменную В зависимости от значения дискриминанта этого квадратного уравнения оно может иметь от 0 до 2 корней. И, соответственно, исходное уравнение может иметь две серии решений, одну или ни одной. Рассмотрим пример. Пример 2. Решить уравнение: Решение: 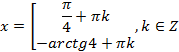 . .Ответ: 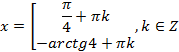 . .Даже если исходное тригонометрическое уравнение второй степени не является однородным, можно его преобразовать к такому виду. Рассмотрим это сначала на примере уравнения второй степени. Пример 3. Решить уравнение: Решение: Сначала умножим 3 на тригонометрическую единицу, то есть на выражение ( Теперь преобразуем полученное уравнение к однородному виду: Теперь решим полученное однородное уравнение: 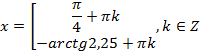 . .Ответ: 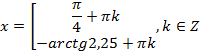 . .3. Теперь рассмотрим, как можно привести к однородному уравнение вида Рассмотрим это на примере. Пример 4. Решение: Используем формулы двойного аргумента: Подставим их в исходное уравнение и домножим на тригонометрическую единицу 2, стоящую в правой части. 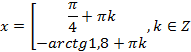 . .Ответ: 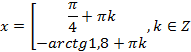 . .Заметим, что подобные уравнения можно решить и по-другому, а именно, применив формулу вспомогательного аргумента: Рассмотрим решение примера 4 этим способом. Пример 4-а. Решение: Преобразуем левую часть: Ответ: Мы видим, что результат, полученный при решении разными способами, кажется разным. Но на самом деле в тригонометрии одно и то же число может быть записано разными способами. Можно сказать, что первый способ в этом случае приводит к более короткому и красивому результату. Решите уравнение Решение: В такой записи уравнение не является однородным. Используем формулу синуса двойного аргумента. Теперь уравнение однородное. Решим его. 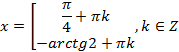 . .Ответ: Решить уравнение 1) с помощью формулы вспомогательного аргумента Решение Ответ: 2) с помощью формул синуса и косинуса двойного аргумента Решение Ответ: 3) Решите уравнение: Решение Ответ: 4. Рассмотрим теперь решение тригонометрических уравнений с использованием универсальной тригонометрической подстановки. Она называется универсальной, так как позволяет любое уравнение вида Универсальная тригонометрическая подстановка – это формулы для выражения синуса, косинуса и тангенса аргумента через тангенс половинного аргумента: 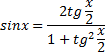 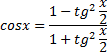 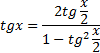 То есть если сразу обозначить Рассмотрим пример 5. Решить уравнение Решение: Область определения исходного уравнения: Преобразуем исходное уравнение: Используем универсальную тригонометрическую подстановку. Если Решим его. Ответ: Заметим, что когда мы используем универсальную тригонометрическую подстановку, у нас появляется тангенс половинного угла, который не всегда определен. Поэтому мы можем потерять корни. Нужно проверить. Так как эти числа, Решите уравнение Рассмотрим решение уравнения Решение: Найдем область допустимых значений: 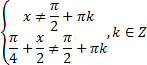 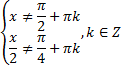 Теперь используем универсальную тригонометрическую подстановку и формулу тангенса суммы аргументов. 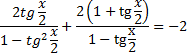 Область допустимых значений полученного уравнения уже, чем исходного: Решим полученное уравнение: Но необходимо проверить те числа, которые выпали из области определения после использования универсальной тригонометрической подготовки. Это числа вида Подставим π в (**): Таким образом, получается ответ. Ответ: Заключение В данной работе были рассмотрены методы решения тригонометрических уравнений, как простейших, так и сложного уровня. Были рассмотрены основные методы решения тригонометрических уравнений, причем, как специфические — характерные только для тригонометрических уравнений, так и общие функциональные методы решения уравнений, применительно к тригонометрическим уравнениям. В моей работе были рассмотрены решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Ввиду того, что решения тригонометрических уравнений можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, рассмотрена общая схема решения тригонометрических уравнений и подробно рассмотрено преобразование групп общих решений тригонометрических уравнений. Результаты данной работы могут быть использованы в качестве учебного материала при составлении факультативов для школьников, так же работа может применяться при подготовке учащихся к вступительным экзаменам и централизованному тестированию. Колягин Ю. М., Ткачева М. В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2014. Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014. Шахмейстер А.Х. Тригонометрия. М. 2014, 712 с. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. - М., 2011. - 287 с. |
