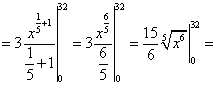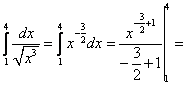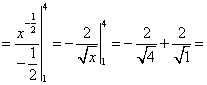ФУНКЦИИ. Тема Функции

• Название: Тема Функции
• Дата: 15.11.2022
• Размер: 1.59 Mb.
• Имя файла: ФУНКЦИИ.docx
• Тип: Документы; #789352
• страница: 16 из 32

Тема 2. Правила вычисления интеграла

Свойства определенного интеграла.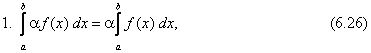



где a — произвольное число.



где a, b и c —любые числа, т.е. если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из частей.

4. Если на отрезке [a ; b] f ( x) ≤ g ( x), то и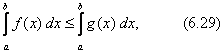



т.е. обе части неравенства можно почленно интегрировать.

5. Теорема о среднем. Если функция y = f ( x) непрерывна на отрезке [a; b], то найдется такое значение   ∈ [a; b], что

Пусть f ( x) ≥ 0 на [ a; b]. Тогда теорема о среднем утверждает: найдется такая точка 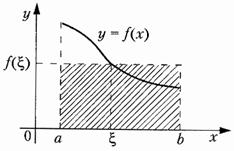  из отрезка [a; b], что площадь под кривой y = f ( x) на [a; b] равна площади прямоугольника со сторонами f (  ) и (b – a) (рис.6.3)



Рис. 6.3.

Определенный интеграл как функция верхнего предела. Если функция y = f ( x) интегрируема на отрезке [a; b], то, очевидно, она интегрируема также на произвольном отрезке [a; x], вложенном в [a; b].

Полагаем по определению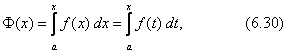



где x ∈ [a; b], а функция Φ (x) называется интегралом с переменным верхним пределом.

Пусть f ( t) ≥ 0 на отрезке [a; b]. Тогда значение функции Φ (x) в точке x равно площади S ( x) под кривой y = f ( t) на отрезке [a; x] (рис.6.4). (В этом состоит геометрический интеграла с переменным верхним пределом).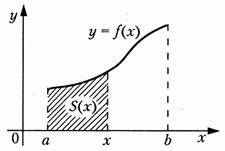



Рис. 6.4.

Теорема. Пусть функция f ( x) непрерывна на отрезке [a; b]. Тогда в каждой точке x отрезка [ a; b] производная функции Φ (x) по переменному верхнему пределу равна подинтегральной функции f ( x), т.е.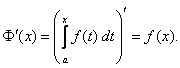



Слествие. Если функция y = f ( x) непрерывна на отрезке [a; b], то для этой функции существует первообразная на отрезке [a; b].

Действительно примером первообразной для f ( x) является функция Φ (x), заданная формулой (6.30).

Замечание. Если f ( x) — элементарная функция, то это еще не означает, что будет элементарной функция Φ (x). Например, функции   (и т.п. функции, связанные с неберущимися интегралами) неэлементарные, так как они являются первообразными для функций   которые не имеют первообразных в классе элементарных функций.

Теорема. Пусть функция y = f ( x) непрерывна на отрезке [a; b] и F ( x) — любая первообразная для f ( x) на [a; b]. Тогда определенный интеграл от функции f ( x) на [a; b] равен приращению любой ее первообразной F ( x) на этом отрезке, т.е.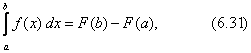



или в иной записи

Формула (6.30) — формула Ньютона – Лейбница— основная формула интегрального исчисления, устанавливающая связь между понятиями определенного и неопределенного интегралов.

Нахождение определенных интегралов с использованием формулы Ньютона – Лейбница (6.31) осуществляется в два шага: на первом шаге, используя технику нахождения неопределенного интеграла, находят некоторую первообразную F ( x) для подинтегральной функции f ( x); на втором — применяют собственно формулу Ньютона – Лейбница и находят приращение первообразной, равное искомому интегралу.

Пример 6.11. Вычислить 

Решение. Произвольная первообразная для функции f ( x) = x² имеет вид   Для нахождения интегралов по формуле Ньютона – Лейбница возьмем такую первообразную у которой C = 0. Тогда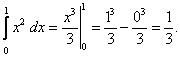



При нахождении интегралов удобно использовать свойство приращения первообразной



где a — произвольное число.

Замена переменной в определенном интеграле. Пусть функция 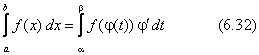  (t) имеет непрерывную производную на отрезке [a ,  ], a =   (a ), b =   ( ) и функция f ( x) непрерывна в каждой точке вида x =   (t), где t ∈ [a ,  ]. Тогда справедливо следующее равенство



— формула замены переменной в определенном интеграле.

В отличие от неопределенного интеграла при вычислении определенного интеграла данным способом нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования a и   новой переменной t как решение относительно переменной t уравнения   (t) = a,   (t) = b.

Пример 6.12. Вычислить 

Решение. Пусть t = 2 – x². Тогда dt = d (2 – x²⁾ = (2 – x²⁾' dx = – 2 xdx и   если x = 0, то t = 2 – 0² = 2, и если x = 1, то t = 2 – 1² = 1. Следовательно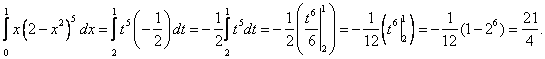



Интегрирование по частям в определенном интеграле. Пусть функции u = u ( x) и v = v ( x) имеют непрерывные производные на отрезке [a; b]. Тогда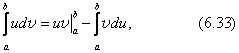



где 

Формула (6.33) называется формулой интегрирование по частям определенного интеграла.

Пример 6.13. Вычислить 

Решение. Пусть u = ln (1 + x), d v = dx. Тогда 

Применяя (6. 33), получаем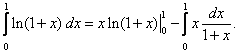



Для нахождения полученного интеграла полагаем 1 + x = t. Тогда dx = dt, x = t – 1 и если x = 0, то t = 1, если x = 1, то t = 2. Следовательно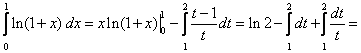





Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 211–216.

Пример 1

Вычислите определенный интеграл: а)  ; б)  ; в)  ; г)  ; д)  ; е)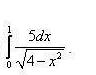 
План решения

Использовать формулу Ньютона-Лейбница   и таблицу интегралов.

Решение	Комментарий
а). б)  . в)  . г)  . д)  . е)  .	Использовать формулу. Использовать формулы: 1.  . 2.. 3.. Сначала преобразовать подынтегральную функцию по формуле. Затем использовать формулы: 1.. 2.. Сначала преобразовать подынтегральную функцию по формуле. Затем использовать формулу. Использовать формулы: 1.  . 2.. 3.. Использовать формулы: 1.. 2..

Цит. по: Методическое пособие-тренажер решения задач по высшей математике /
Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 59–60.

11.1. Вычислить определенные интегралы: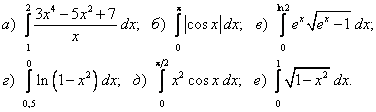



Решение:

а) Используя эквивалентное преобразование подынтегральной функции (почленное деление числителя на знаменатель) и свойства, определенного интеграла, получаем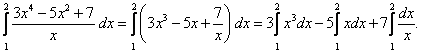



Все три интеграла — табличные; согласно, окончательно имеем: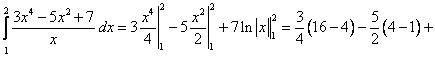



б) Так как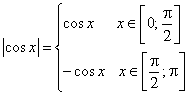



то



(1 – 0) – (0 – 1) = 2.

в) Воспользуемся заменой переменной: пусть  . Тогда t ² = е^х– 1, е^х= t² + 1, 2t dt = e^x dx и   Найдем пределы интегрирования по переменной г. если х = 0, то   если х = ln2, то   Искомый интеграл теперь принимает вид:



г) Воспользуемся формулой интегрирования по частям: пусть u = ln(1 – х²), dv = dx. Тогда 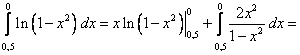 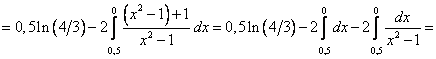 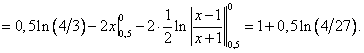и







д) Как было отмечено выше, данный интеграл находится с помощью последовательного применения формулы интегрирования по частям. Пусть и = х², dv = cos xdx.Тогда du = ( x²)'dx = 2х dx,   и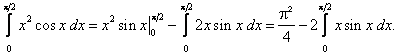



Для нахождения последнего интеграла вновь применяем формулу: и = х, dv = sin x dx. Тогда du = dx,   и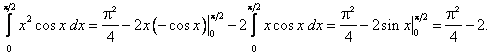



e) Воспользуемся тригонометрической подстановкой х = sin t.Будем полагать, что t ∈ [0; 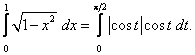 /2]. Если t = 0, то х = 0; если t =  /2, то х = 1. Тогда dx = cos t dt и



Так как cos t > 0 при t ∈ [0; 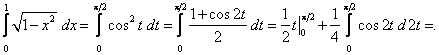 /2], то |cos t| = cos t. Применяя тригонометрическую формулу понижения степени, получаем:





Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 290–291.
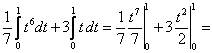
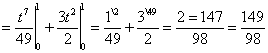