Решение Пусть событие а кость, наудачу извлеченная из полного набора домино, имеет сумму очков, равную пяти
 Скачать 139.5 Kb.
|
|
Вариант 8 1. На десяти жетонах выбиты числа 1; 2; 3; ...; 10. Наудачу извлекается один жетон. В каких из следующих ответов указаны все возможные исходы испытания: а) {четное; 1; 3; 5}, б) {не более трех; не менее четырех}? Решение: б) {не более трех; не менее четырех} = {1,2,3,4,5,6,7,8,9,10}. 2. Какова вероятность того, что кость, наудачу извлеченная из полного набора домино, имеет сумму очков, равную пяти? Решение: Пусть событие А - кость, наудачу извлеченная из полного набора домино, имеет сумму очков, равную пяти. Всего  костей домино.Из них  имеют сумму очков, равную пяти (0,5), (1,4), (2,3). .Ответ: .3. Из двух полных наборов шахмат наудачу извлекают по одной фигуре или пешке. Какова вероятность того, что обе фигуры окажутся слонами? Решение: В каждом из двух наборов по 32 шахматные фигуры и по 2 слона. Вероятность того, что игрок вытащит слона из первого набора шахмат =  (событие А).Вероятность того, что игрок вытащит слона из второго набора шахмат = (событие В). События А и В — независимые, поэтому вероятность того что обе фигуры окажутся слонами равна:  .Ответ:  .4. Сколько различных трехбуквенных «слов» можно составить из букв слова РОМБ? Решение: Различные комбинации трех букв из имеющихся четырех представляют размещения, так как могут отличаться как составом входящих букв, так и порядком их следования,  .Ответ: 24 слова. 5. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, французского, немецкого, итальянского на любой другой из этих пяти языков? Решение: Поскольку важен порядок, с какого языка задается перевод на другой, то для ответа на вопрос необходимо найти число размещений из пяти по два  .Ответ: 20 словарей. 6. Трое юношей и две девушки выбирают место работы. Сколькими способами они могут это сделать, если в городе есть три завода, где требуются рабочие в литейные цехи (туда берут лишь мужчин), две ткацкие фабрики (туда приглашают женщин) и две фабрики, где требуются мужчины и женщины? Решение: Два места работы для девушек можно отобрать из 4 мест работы  способами; отобрать три места работы для юношей из пяти мест работы можно  способами.Следовательно, число благоприятствующих исходов равно  .Ответ: 60 способов. 7. В коробке находятся 4 красных и 6 зеленых карандашей. Из нее случайно выпали 3 карандаша. Какова вероятность того, что два из них окажутся красными? Решение: Пусть событие А - два из трех карандашей окажутся красными. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно отобрать 3 карандаша из 10, т.е. числу сочетаний из 10 элементов по 3 элементов (  ).Определим число исходов, благоприятствующих интересующему нас событию А. Два красных карандаша можно отобрать из 4 красных способами; отобрать же один зеленый карандаш из 6 можно  способами.Следовательно, число благоприятствующих исходов равно  .Искомая вероятность равна: 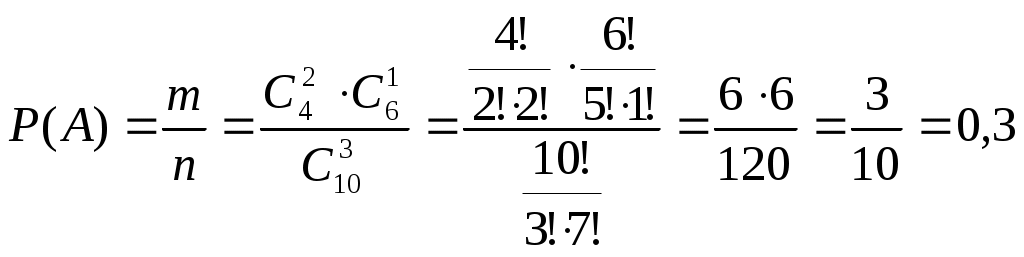 .Ответ:  .8. Мишень имеет форму окружности радиуса 4. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены. Решение: 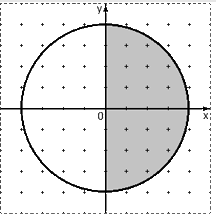 Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем:  .Ответ:  .9. Студент знает ответы на 15 экзаменационных билетов из 20. В каком случае он имеет большую вероятность сдать экзамен, если он идет отвечать первым или если - вторым? Решение: Пусть событие А - студент идет отвечать первым. Пусть событие В - студент идет отвечать вторым.  .Если студент идет отвечать вторым, то первый студент мог выбрать либо билет, на который студент знает ответ, либо билет на который студент не знает ответ  .Ответ: в обоих случаях. 10. По одному и тому же маршруту в один и тот же день совершают полет 3 самолета. Каждый самолет с вероятностью 0,7 может произвести посадку по расписанию. Для случайного числа самолетов, отклонившихся от расписания, составьте таблицу распределения вероятностей. Решение: Случайная величина Х может принимать значения: 0,1,2,3. Вычислим вероятности значений случайной величины Х по формуле Бернулли:  В нашем случае: n = 3, p=0,7, q = 0,3.  ; ; ; .Составим закон распределения числа самолетов, отклонившихся от расписания - Х:
11. Набрасываются кольца на колышек или до первого попадания или до полного израсходования всех колец, число которых равно пяти. Покажите, что если вероятность набросить каждое кольцо на колышек равна 0,9, то математическое ожидание случайного числа брошенных колец равно 1,1111. Решение: Так как вероятность попадания кольца на колышек равна 0,9, то вероятность промаха равна 1-0,9=0,1. Пусть Х – случайная величина – число брошенных колец. Х может принимать любые натуральные значения от 1 до 6 включительно. Найдём вероятности, соответствующие каждому из значений случайной величины.  – бросил первое кольцо и попал; – первое кольцо промах, а вторым попал; – первые два кольца промах, а третьим попал; – первые три кольца промах, а четвёртым попал; – первые четыре кольца промах, а пятым попал; – первые пять колец промах, а шестым попал или все шесть колец промах. Таким образом, ряд распределения числа брошенных колец имеет вид:
Сумма  называется математическим ожиданием дискретной случайной величины и обозначается  . ;  . 12. Случайная величина X подчинена нормальному закону распределения с математическим ожиданием, равным 50. Определите дисперсию случайной величины X, если известно, что вероятность принятия случайной величиной значения в интервале ]50;60[ равна 0,3413. Решение: Вероятность попадания в заданный интервал нормальной случайной величины:  .Случайная величина X подчинена нормальному закону распределения с математическим ожиданием, равным  . ; ; ;  . - дисперсия случайной величины X. |
