математика. Решение_AU_6701230. Решение Пусть, тогда приходим к уравнению
 Скачать 231 Kb. Скачать 231 Kb.
|
|
Министерство науки и высшего образования Российской федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Комсомольский-на-Амуре государственный университет» Факультет Кадастра и строительство Кафедра «Математика» КОТРОЛЬНАЯ РАБОТА по дисциплине «Математика» Вариант №1 Студент группы 0ПСба-1 Ш.Р. Амиров Преподаватель М.В. Сташкевич 2021 Задание 1 Найти общее решение дифференциального уравнения первого порядка. Решение Данное уравнение линейное, найдём его общее решение методом Бернулли. Сделаем подстановку Подставляя найденную функцию в уравнение получим второе дифференциальное уравнение с разделяющимися переменными, из которого найдём функцию Задание 11 Найти общее решение дифференциального уравнения второго порядка Решение Пусть Это уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем: 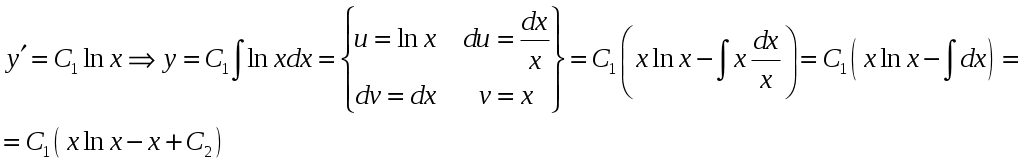 Задание 31 Найти частное решение дифференциального уравнения Решение Найдём сначала общее решение соответствующего однородного уравнения Правая часть неоднородного уравнения имеет вид Подставляя эти выражения в неоднородное уравнение (с правой частью fx): 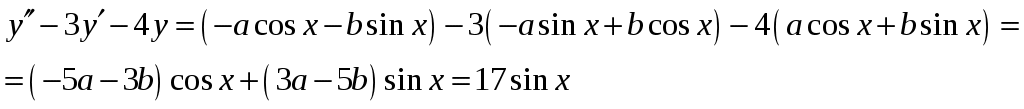 Приравниваем коэффициенты при одинаковых степенях x и находим: 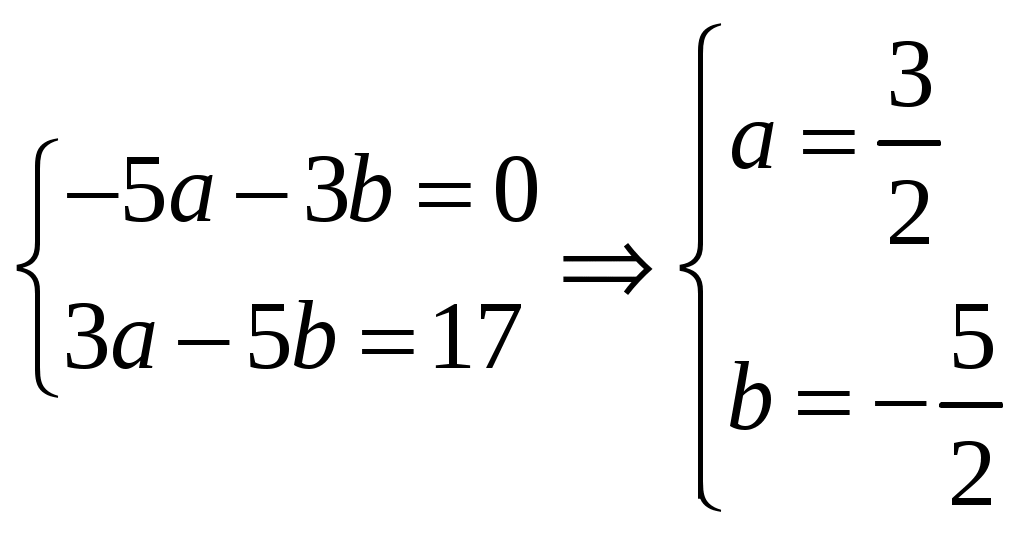 . Таким образом, . Таким образом, Найдем частное решение 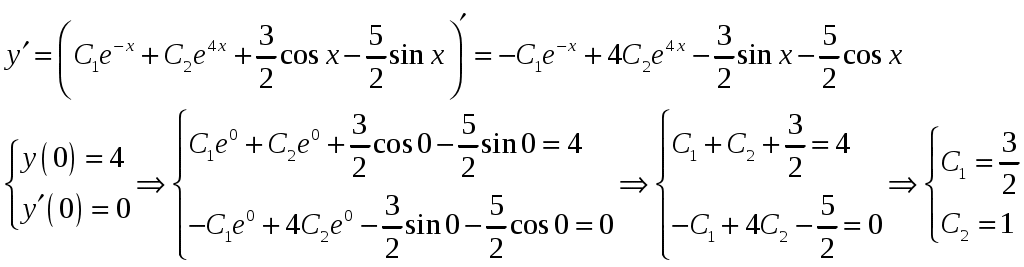 Значит, частное решение есть Задание 61 Исследовать ряд на сходимость А) Решение А) Применим предельный признак сравнения 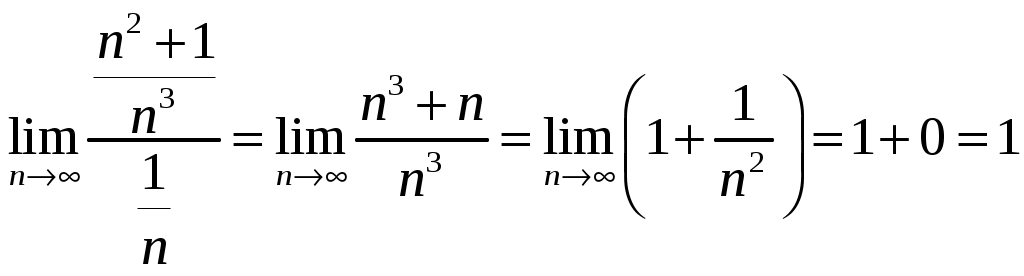 , значит, в силу конечности предела и расходимости , значит, в силу конечности предела и расходимости Б) Рассмотрим сразу ряд из модулей 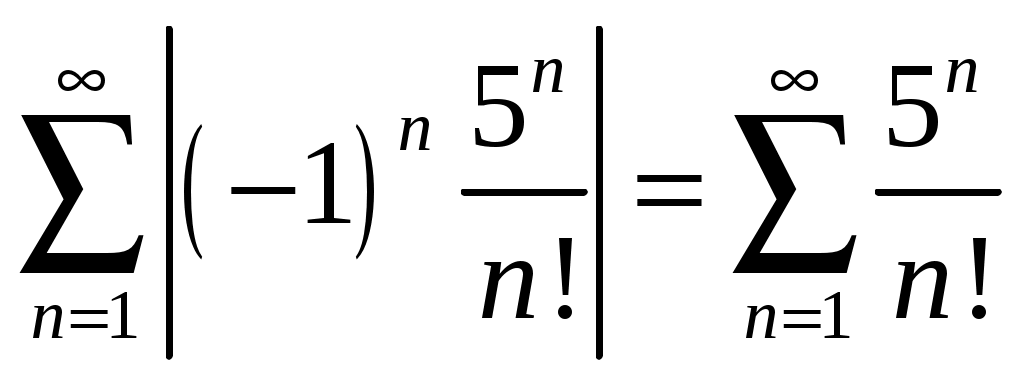 . Для ряда . Для ряда 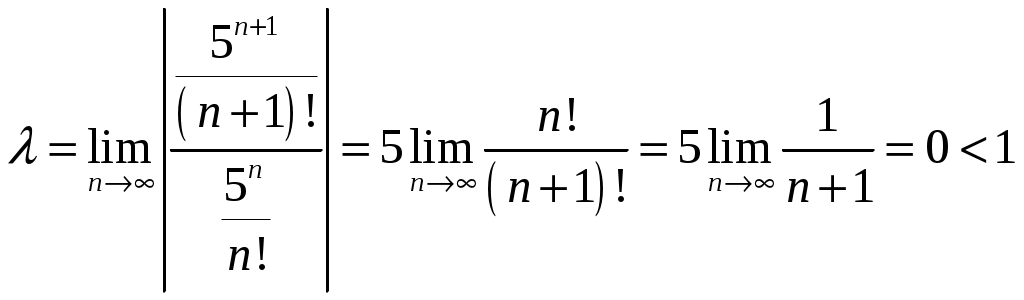 , значит, ряд , значит, ряд Задание 71 Найти область сходимости степенного ряда Решение Из признака Даламбера получаем 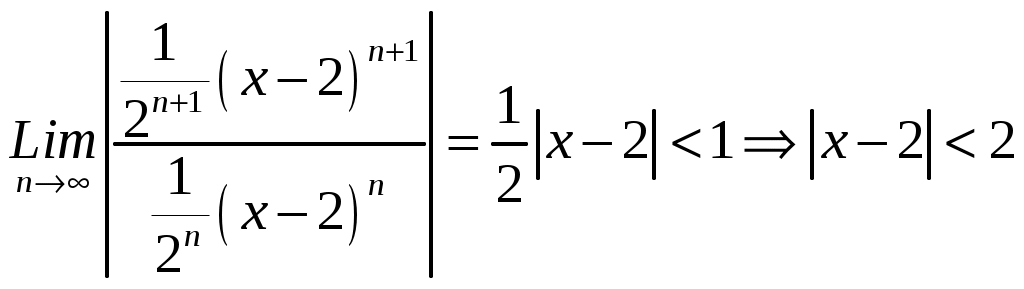 , значит, радиус сходимости равен 2, интервал сходимости , значит, радиус сходимости равен 2, интервал сходимости При Так как Задание 91 Найти 3 первых членов разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего начальным условиям Решение 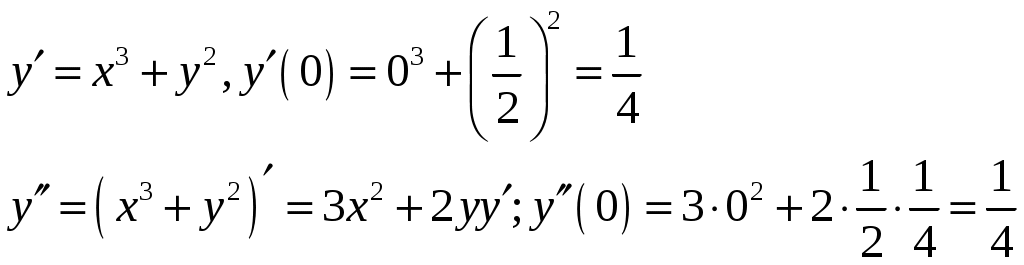 Ряд Тейлора имеет вид 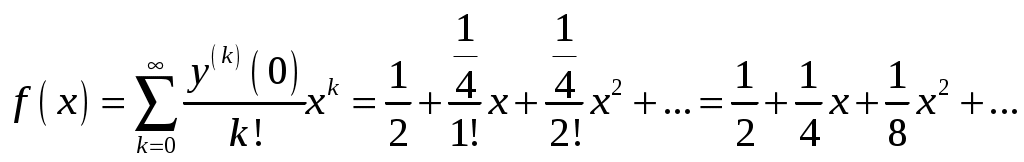 Задание 101 Разложить в ряд Фурье функцию f(x), периодическую, с периодом 2, заданную на промежутке (–, ] следующими равенствами Решение Перед вычислением коэффициентов Фурье вычислим вспомогательный интеграл 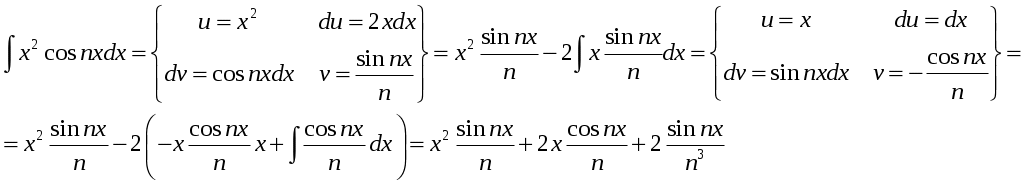 Ряд Фурье для функции В данном случае Так как функция четная, поэтому 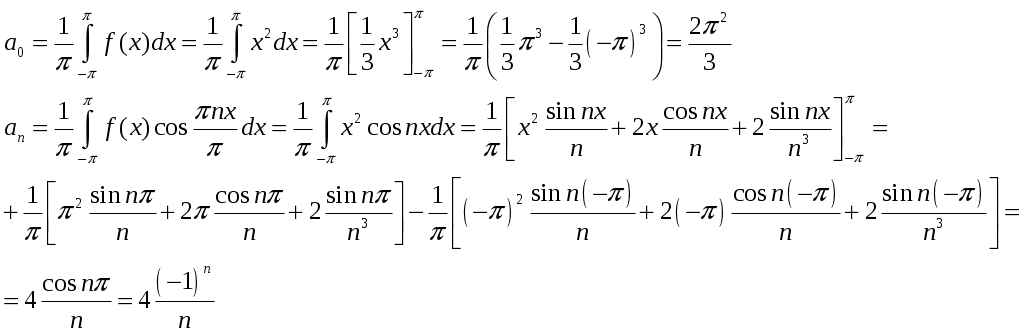 Значит, 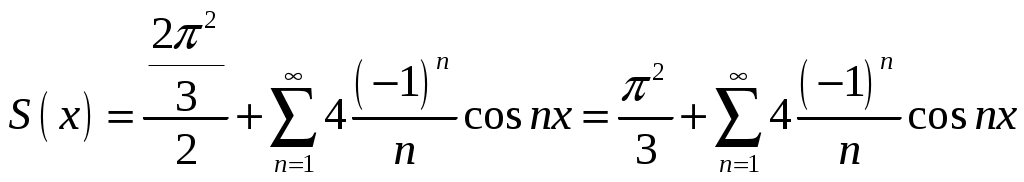 |
