Решение р 20 ф (20 ) 0 Найдя значение функции ф (z) по таблицам, находим значение аргумента

• Название: Решение р 20 ф (20 ) 0 Найдя значение функции ф (z) по таблицам, находим значение аргумента
• Дата: 23.02.2023
• Размер: 77.04 Kb.
• Имя файла: 13238353_Vrezul_tatepove.docx
• Тип: Решение; #951501

1. 
   В результате поверки вольтметра установлено, что 60% погрешностей результатов измерений, произведенных с его помощью, не превосходит ±20 мВ . Считая, что погрешность распределена по равномерному закону с нулевым математическим ожиданием, определить среднюю квадратическую погрешность S.
   

Решение:

Р [    20 ] = Ф (20 / ) = 0,7.

Найдя значение функции Ф (z) по таблицам, находим значение аргумента:

20 /  = 1,04,

откуда  = 19 мА.

2. 
   Показания цифрового омметра с пределом шкалы 1000 Ом — R = 910 Ом. Из паспортных данных прибора известно, что систематическая погрешность составляет ±(0,2% + стоимость 1 единицы младшего разряда кода R), дополнительная температурная погрешность ΔRt = ±1 Ом, среднеквадратическое отклонение случайной погрешности S = 0,7 Ом. Записать результат измерения.
   

Решение: Для расширения шкалы в n раз измерений вольтметру последовательно подключают добавочное сопротивление, величина которого рассчитывается по формуле:

R доб = R V · (n − 1), где

RV — внутреннее сопротивление вольтметра;

n – коэффициент расширения предела измерения:

n = UUO ,

U0 — максимальное напряжение, которое можно было измерять до подключения добавочного сопротивления;

U — максимальное напряжение, которое необходимо измерять данным вольтметром (после подключения добавочного сопротивления).

R доб = 1000 ·( 101 -1) = 9000 Ом = 9 кОм

Основная погрешность прибора с добавочным резистором:

δR = КТR · 100 % = 0,59000 · 100 % = ± 0,01 %

Ответ: δR = ± 0,01 %

3. 
   Вольтметр имеет предел измерения Uшк1 =1В , класс точности γ1 = 1.0 ,входное сопротивление Rv = 1 кОм .Рассчитать величину и допустимую относительную погрешность добавочного сопротивления, необходимого для изменения предела измерения до Uшк2 = 10 В и достижения общего класса точности γ2 = 0.5
   

Решение:

Для расширения шкалы в n раз измерений к вольтметру подключают последовательно добавочное сопротивление, которое рассчитывается по формуле:


RV- внутреннее сопротивление вольтметра

n-Коэффициент расширения предела измерения

n=UUO

UO-максимальное напряжение, которое можно было измерять до подключения добавочного сопротивления

U-максимальное напряжение, которое необходимо было измерять данным вольтметром.

Rдоб=1000*(100-1)=9000 Ом=9кОм

Основная погрешность прибора с добавлением резистора

δR=KRT*100%=0,59000*100%=±0,01%

Ответ: ±0,01%

4. 
   При многократных измерениях ёмкости получены следующие
   

результаты: 40; 40.4; 40.8; 39.2; 39.6; 40; 39.6; 40.4; 36.8; 40 пФ .

Записать результат измерения при доверительной вероятности PД =0.95 .

Решение:

Подсчитываем количество наблюдений: n =10 . Так как при n = 15 20 − невозможно идентифицировать закон распределения, то этот пункт из стандартного алгоритма обработки многократных измерений опускаем. Используем упрощенный алгоритм обработки, который начинается с пункта:

1. 
   Удалениепромахов. Условие промаха
   

• 
  t_гр(Р_Д
  

, n) ,

где

X_i — подозрительный на наличие промаха результат изме-

рения из полученной выборки;

t_гр(Р_Д, n)

— коэффициент до-

пускаемых нормированных отклонений (границы интервала

цензурирования), выбирается при заданных Р_Д

Приложения. Определяем для нашей задачи

и nиз таблицы П.2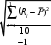


10 _R

R ⁱ 39,68 Пф;

i1 ¹⁰

S  0,35 Пф.

Зададимся доверительной вероятностью

Р_Д = 0,95 (реко-

мендуется брать 0,9—0,99) и из таблицы П.2 Приложения най- дем t_гр(0, 95;40)  2, 414 . Промахи удаляют итеративно, по од-

ному. Начинают проверку

R_i с величины, наиболее отстоящей

от R. В нашей задаче это R_i= 40,8. Тогда

40,839,68 _{ 3,2  t}

0,35 ^гр

 2, 414 .

Условие промаха выполняется, то есть

R_i= 40,8 — промах.

Его удаляем из ряда многократных измерений. Теперь

n 9 .

Продолжаем проверку на наличие промахов. Пересчитываем вновь значения

9 _R

R _ⁱ 39,6П Ом

и S  0,20Пф.

i1 ⁹

Опять находим наиболее удаленные от Rзначения

R_i. Это

39,6 и 40,4, причем они равноудалены от R. Проверяем, являют- ся ли они промахами. По таблице определяем новые границы

цензорского интервала

t_гр(0, 95;9)  2, 349 . Условие промаха

39,640

0,20

 2 2, 349

Не выполняется, то есть

R_i= 39,6 и

R_i= 40,4 (т.к. цензорский интервал симметричен) не являются

промахами. Все остальные R_i

расположены к Rеще ближе,

следовательно, тем более не являются промахами, их индивиду- альная проверка нецелесообразна.

2. 
   
   Результатизмерения,погрешность.За результат изме- рения принимается среднее арифметическое ряда наблюдений
   

без промахов R= 40 Пф. Границы доверительного интервала погрешности

 t

_S(Р_Д

, n)  S_R

 t_S(Р_Д

, n)  .

Здесь t_S(Р_Д, n)

— коэффициент Стьюдента, выбирается из

таблицы П.3 Приложения. В нашем случае Тогда
t_S(0, 95, 9)  2, 306 .

 2,306 ^0,20  0, 154Пф

Результат измерения в соответствии с правилами представ- ления результата запишем следующим образом:

R_изм (40  0, 154) Пф;

Р_Д 0, 95;

n 9.