ТВ и МС практика. Задачи ТВ. Решение Расчет вероятности взаимосвязанных событий. Вероятность выбора первой буквы Р
 Скачать 20.45 Kb. Скачать 20.45 Kb.
|
|
Задачи: 1. Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках; карточки перемешаны и положены в пакет. 1.1.Чему равна вероятность того, что, вынимая четыре буквы, ПОЛУЧИМ слово РЕКА? Решение: Расчет вероятности взаимосвязанных событий. Вероятность выбора первой буквы Р: Количество событий = общему количеству букв = 6. Из них благоприятных событий (подходящих букв) = 1. Вероятность по формуле Лапласа: Р = 1 / 6. Вероятность, что вторая буква Е: Р = 1/5 (из оставшихся 5ти букв 1 Е); Вероятность того, что третья буква будет К: Р = 1/4 (из оставшихся 4х букв 1 К); Вероятность того, что четвертая буква будет А: Р = 2/3 (из оставшихся 3х букв 2 А); Ответ: вероятность взаимосвязанных событий, что поочередно вынуты буквы Р, Е, К, А: Р = (1 / 6) * (1 / 5) * (1 / 4) * (2 / 3) =2/360 = 1/180 = 0,005 1.2.Какова вероятность сложить слово КАРЕТА при вынимании всех букв? Решение: Расчет вероятности взаимосвязанных событий. Вероятность выбора первой буквы К: Количество событий = общему количеству букв = 6. Из них благоприятных событий (подходящих букв) = 1. Вероятность по формуле Лапласа: Р = 1 / 6. Вероятность того, что вторая буква будет А: Р = 2/5 (из оставшихся 5ти букв 2 А); Вероятность того, что третья буква будет Р: Р = 1/4 (из оставшихся 4х букв 1 Р); Вероятность того, что четвертая буква будет Е: Р = 1/3 (из оставшихся 3х букв 1 Е); Вероятность того, что пятая буква будет Т: Р = 1/2 (из оставшихся 2х букв 1 Т); Ответ: вероятность взаимосвязанных событий, что поочередно будут вынуты буквы К,А,Р,Е,Т, А: Р = (1 / 6) * (2 / 5) * (1 / 4) * (1 / 3)*(1 / 2) = 2/720 = 1/360= 0,0027 2. Дискретная случайная величина ξ задана следующим законом распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. Решение: Математическое ожидание: M(ξ)= 4*0,4+6*0,1+10*0,2+12*0,3 = 1,6+0,6+ 2+3,6= 7,8 Дисперсия: D(ξ)= (4-7,8)2 *0,4+(6-7,8)2*0,1+(10-7,8)2*0,2+(12-7,8)2*0,3=5,776+0,324+0,968+5,292= 12,36 Квадратичное отклонение: δ= 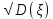 = =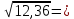 3,515 3,5153. Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание M(ξ) = 1,9, а также M(ξ2) = 7,3, найти вероятности p1, p2, p3, которые соответствуют дискретным значениям случайной величины. Решение: Случайная величина ξ принимает только 3 значения, соответствующие события образуют полную группу, поэтому: p1+ p2 + p3 =1 M(ξ) = -2p1 + p2 +4p3 = 1,9 - по условию задачи M(ξ2) = 4p1 +p2 +16p3 = 7,3 – по условию задачи Решим систему линейных уравнений методом Крамера 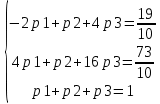 Δ = 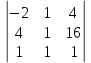 =(−2)⋅1⋅1+1⋅16⋅1+4⋅4⋅1−1⋅1⋅4−1⋅16⋅(−2)−1⋅4⋅1 = 54 =(−2)⋅1⋅1+1⋅16⋅1+4⋅4⋅1−1⋅1⋅4−1⋅16⋅(−2)−1⋅4⋅1 = 54Δ1 = 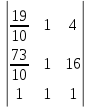 = = 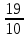 ⋅1⋅1+1⋅16⋅1+4⋅( ⋅1⋅1+1⋅16⋅1+4⋅(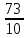 )⋅1−1⋅1⋅4−1⋅16⋅( )⋅1−1⋅1⋅4−1⋅16⋅(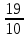 )−1⋅( )−1⋅(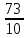 )⋅1= )⋅1=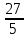 Δ2 = 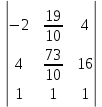 = (−2)⋅( = (−2)⋅(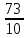 )⋅1+ )⋅1+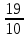 ⋅16⋅1+4⋅4⋅1−1⋅( ⋅16⋅1+4⋅4⋅1−1⋅(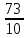 )⋅4−1⋅16⋅(−2)−1⋅4⋅( )⋅4−1⋅16⋅(−2)−1⋅4⋅(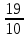 )=27 )=27Δ3 =  = (−2)⋅1⋅1+1⋅( = (−2)⋅1⋅1+1⋅(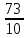 )⋅1+ )⋅1+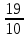 ⋅4⋅1−1⋅1⋅( ⋅4⋅1−1⋅1⋅(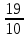 )−1⋅( )−1⋅(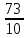 )⋅(−2)−1⋅4⋅1= )⋅(−2)−1⋅4⋅1=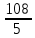 P1 = Δ1 /Δ = 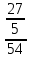 = = 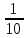 ; ;P2 = Δ2 /Δ = 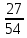 = = 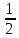 ; ;P3 = 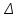 3 /Δ = 3 /Δ = 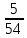 = = 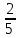 Ответ: р1 = 0,1; р2 = 0,5; р3 = 0,4. |
