Решение Разбиваем стержень на три участка a B, bc, cd
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
|
Задача 1 Для заданной схемы нагружения стержня постоянного сечения ( рис. 1-пр) F=5,0 кН 1) – построить эпюры внутренних сил; - построить в общем виде эпюры напряжений; - определить опасный участок; - из условия прочности (max = ) = 120 МПа определить размер сечения; - определить напряжения на участках стержня и построить эпюры напряжений стержня. 2) определить размеры равнопрочного стержня и экономию материала при равнопрочном стержне. 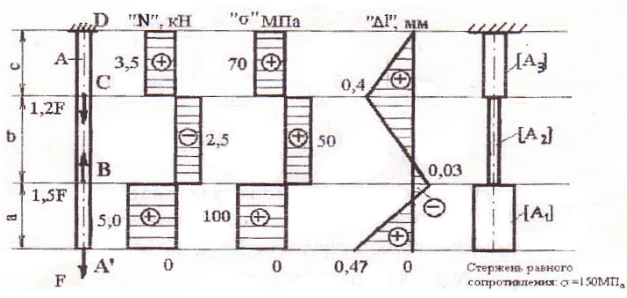  Рис.1-пр Решение: 1. Разбиваем стержень на три участка: A׳B, BC, CD. 2. Определяем внутренние силы на каждом участке стержня. N1 = N(AB) =F = 5,0 kH N2 = N(BC) = F-1,5F = -2,5 kH N3 = N(CD) = F-1,5F+1,2F = 0,7F = 3,5kH 3. Определяем напряжения на каждом участке. (1) = (II) = (III) = 4. Определяем опасный участок. Опасный участок АВ, где действует сила N1=Nmax=F=5,0 kH 5. Из условия прочности определим площадь сечения. Принимаем А= 50 мм2 6. Определяем численные значения напряжений (2)= (3)= По полученным данным строим эпюру напряжений 7. Определяем перемещения на участках стержня Е- модуль продольной упругости, Е= 2105 МПа (для стали) По полученным данным строим эпюру перемещений. 8. По полученным данным определяем размеры сечений равнопрочного стержня, у которого напряжения на каждом участке i=, i = 1,2,3. 9. Определяем экономию материала в равнопрочном стержне. Вес стержня с постоянным сечением, - удельный вес. Вес равнопрочного стержня. Задача 2 Для заданной схемы нагружения вала (рис. 2-пр) - построить эпюры крутящих моментов; - найти опасные сечения ; - определить диаметр вала из условия прочности; - определить углы закручивания на участках вала, построить эпюру углов закручивания ; - проверить вал на жесткость, если 1 M=50 кHм, =80МПа, а=1,0 м Решение: 1. Разбиваем вал на участки: 1-й – АВ, 2-й – ВС, 3-й – СД. Рассмотрим 1-й участок АВ Проводим сечение 1-1 и рассмотрим равновесие отсеченной части и определяем крутящий момент в сечении 1-1 Мм1 = М Проводим сечение 2-2 и определяем крутящий момент в сечении 2-2. Mk2=M-3M=-2M  Рис.2.1-пр. 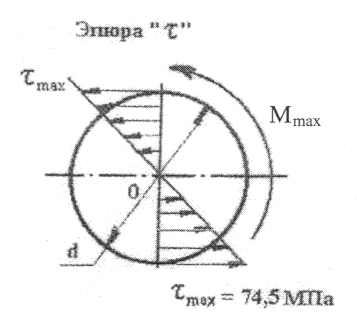 рис. 2.2-пр Крутящий момент в сечении 3-3 Mk3=M-3M+1,5M=-0,5M По полученным данным строим эпюру “Mk” 2. Определяем опасное сечение. Опасными сечениями являются все сечения участка 2, где Mmax= Mk = 2M=100 kHм 3.Определяем диаметр вала из условия прочности Откуда полярный момент сопротивления 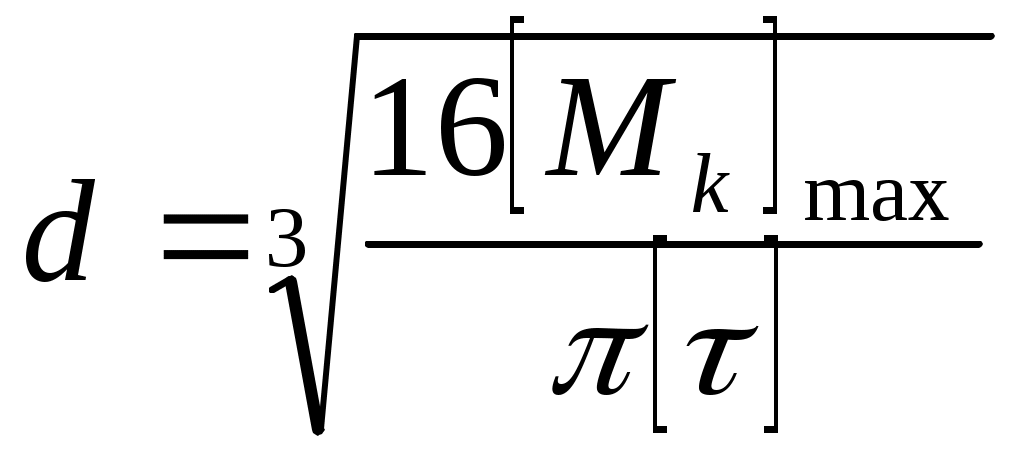 = =Принимаем d=190 мм 4.Определяем углы закручивания на участках вала li – длина участка : a; 1,5а; 0,8а G – модуль упругости при сдвиге G= 0,8 105 МПа J - полярный момент инерции вала J = угол закручивания на участке 3: угол закручивания на 2-ом участке: угол закручивания на 1-ом участке: 5.Определяем относительные углы закручивания 1; 0,281 2= 6.Определим диаметр вала из условия прочности Округляем диаметр d = 130 мм. Применяем диаметр вала d=190мм,удовлетворяющий условиям прочности и жесткости Задача 3 При заданной схеме нагружения стальной балки двутаврового сечения (рис. 3-пр) построить эпюры Q(x) и M(x) определить величины заданных внешних нагрузок q, F и M. Дано: Решение: 1. Определяем опорные реакции  Рис. 3-пр 2. Разбиваем балку О на 3 участка (АС; СD; DB) Участок АС(0 x1 a) Q  (x1) = RA - q x1; Mx1 = RA x1 – q x1 (x1) = RA - q x1; Mx1 = RA x1 – q x1x1=0; Q(0) = RA = 0,6q x1=0; M(0) = 0 x1=a; Qa = RA – qa = 0,6q-q =-0,4q x1=a; M(a) = 0,6q 1-q Находим Мmax. RA - q M(x1)max=0,6q 0,6 - Участок CD (a x2 2a)  = У  часток DB (0 x3 a) часток DB (0 x3 a)По полученным результатам строим эпюры Q и M. В точке d эпюры изгибающих моментов. По заданной величине допустимого напряжения = 150 МПа определяем величины предельных нагрузок. Для двутавра №18 Задача 4 Для заданной схемы нагружения стержня, у которого: l = 6м; F = 700kH ; = 160МПа; ( рис.-4-пр) Найти: а, Fкр  Рис.4-пр Решение: 1. Определяем осевые моменты инерции: 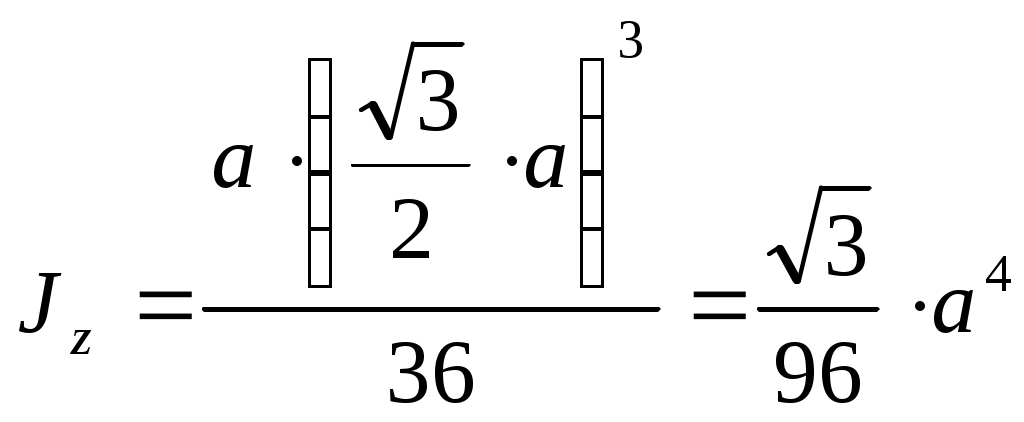 ; ;  2.Определяем радиус инерции сечения:  Площадь сечения: 3.Определяем размер сечения из условий устойчивости: - Первое приближение: принимаем о = 0,5 Площадь сечения: Сторона сечения: Радиус инерции сечения: Гибкость стержня: 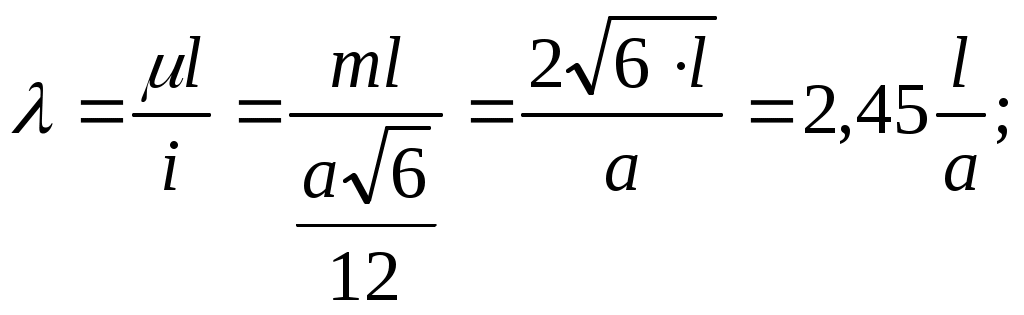 - коэффициент приведенной длины стержня; = По таблице 1.13, Дарков и Шпиро, “Сопротивление материалов” - = f(); 1= 0,58 - Второе приближение: Следовательно, при а=136 мм стержень удовлетворяет условию устойчивости. - Определяем критическую силу:  Определяем коэффициент запаса по устойчивости: |
