лекция. 5 лекция. Лекция
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
5. Лекция. Чистый сдвиг. Кручение стержня круглого поперечного сечения. Напряжения и деформации при чистом сдвиге. Кручение стержня с круглым поперечным сечением. Геометрические характеристики поперечных сечений. Внутренние силовые факторы при изгибе. Статические моменты и центр тяжести плоской фигуры. 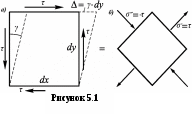 Чистый сдвиг – это напряженное состояние, при котором на гранях выделенного из тела элемента возникают только касательные напряжения (рисунок 5.1 а). Однородный чистый сдвиг имеет место при кручении тонкостенной трубки (рисунок 5.2). Чистый сдвиг – это напряженное состояние, при котором на гранях выделенного из тела элемента возникают только касательные напряжения (рисунок 5.1 а). Однородный чистый сдвиг имеет место при кручении тонкостенной трубки (рисунок 5.2).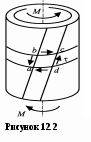 Можно доказать, что если из элемента, находящегося в условиях чистого сдвига, вырезать элемент с гранями, наклоненными под углами в 45º к исходным граням, то на них касательных напряжений не будет, а будут иметь место только нормальные напряжения (рисунок 5.1 б). При этом на одной паре противоположных граней напряжения являются растягивающими (σ’=), на другой – сжимающими (σ”=). Можно доказать, что если из элемента, находящегося в условиях чистого сдвига, вырезать элемент с гранями, наклоненными под углами в 45º к исходным граням, то на них касательных напряжений не будет, а будут иметь место только нормальные напряжения (рисунок 5.1 б). При этом на одной паре противоположных граней напряжения являются растягивающими (σ’=), на другой – сжимающими (σ”=).Как отмечалось ранее, касательные напряжения связаны с угловой деформацией γ законом Гука =G∙γ. (5.1) Можно доказать, что при чистом сдвиге стороны элемента не изменяют своей длины при деформировании, изменение объема также равно нулю. Аналогично испытаниям материала на растяжение и сжатие, проводят испытание на чистый сдвиг. Для этого используют тонкостенные трубки, закручиваемые моментами. В результате получают условную диаграмму сдвига в координатах и γ, которая имеет сходство с диаграммой растяжения, при этом для пластичных металлов предел текучести т=(0,5…0,55)σт. Напряженное состояние, близкое к чистому сдвигу, возникает в заклепках, болтах (устанавливаемых без зазора), шпонках, шлицах, сварных швах. Кручение стержня с круглым поперечным сечением 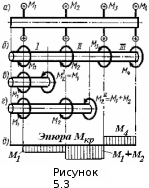 Под кручением понимается такой вид нагружения стержня, при котором в его поперечных сечениях возникает только крутящий момент Мкр, а остальные ВСФ равны нулю. Кручение обычно возникает при нагружении стержня парами сил (скручивающими моментами), плоскости действия которых перпендикулярны продольной оси стержня. Эпюру крутящего момента строят с использованием метода сечений, при этом Мкр равен сумме моментов относительно продольной оси стержня всех пар сил, расположенных по одну сторону от рассматриваемого сечения Под кручением понимается такой вид нагружения стержня, при котором в его поперечных сечениях возникает только крутящий момент Мкр, а остальные ВСФ равны нулю. Кручение обычно возникает при нагружении стержня парами сил (скручивающими моментами), плоскости действия которых перпендикулярны продольной оси стержня. Эпюру крутящего момента строят с использованием метода сечений, при этом Мкр равен сумме моментов относительно продольной оси стержня всех пар сил, расположенных по одну сторону от рассматриваемого сечения Мкр = ∑Mi. (5.2) Правило знаков: если наблюдатель со стороны внешней нормали к сечению видит момент Мкр направленным против часовой стрелке, то он считается положительным, иначе - отрицательным. Внешние моменты в (5.2) должны браться с противоположным правилом. На рисунке 5.3 показан пример построения эпюры Мкр. При расчете стержня (вала) обычно требуется определить напряжения и угловые перемещения в зависимости от величин внешних моментов. Методами СМ можно получить решение только для стрежня кругового или кольцевого поперечного сечения (будем рассматривать только этот случай) и для тонкостенных стержней. 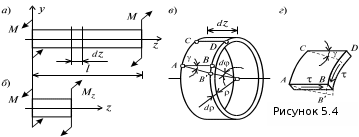 В случае кручения стержня с круговым поперечным сечением будем считать, что каждое поперечное сечение стержня поворачивается в своей плоскости на некоторый угол как жесткое целое (гипотеза плоских сечений). В случае кручения стержня с круговым поперечным сечением будем считать, что каждое поперечное сечение стержня поворачивается в своей плоскости на некоторый угол как жесткое целое (гипотеза плоских сечений).Рассмотрим стержень с круговым поперечным сечением, нагруженный по концам моментами M (рисунок 5.4 а). В его поперечных сечениях возникает постоянный крутящий момент Мкр=M. Двумя поперечными сечениями, выделим из стержня элемент длиной dz, а из него свою очередь двумя цилиндрическими поверхностями с радиусами и ( + d) –элементарное кольцо, показанное на рисунке 5.4 в. В результате кручения правое торцевое сечение кольца повернется на угол d. При этом образующая цилиндра АВ повернется на угол и займет положение АВ. Дуга BВ равна с одной стороны, ∙d, а с другой стороны ∙dz. Следовательно, 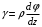 . (5.3) . (5.3)Угол 0 представляет собой угол сдвига цилиндрической поверхности под действием касательных напряжений . Величину 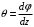 (5.4) (5.4)называют относительным углом закручивания. Это угол взаимного поворота двух сечений, отнесенный к расстоянию между ними. Из рассмотрения (5.3) и (5.4) получим =∙θ0. (5.5) По закону Гука для сдвига τ=G∙θ (5.6) где касательные напряжения в поперечном сечении стержня. Парные им напряжения возникают в продольных плоскостях (рисунок 12.4 г). 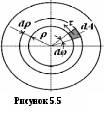 Очевидна (рисунок 5.5) зависимость Очевидна (рисунок 5.5) зависимость 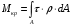 . С учетом (5.6) получаем . С учетом (5.6) получаем 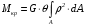 . Интеграл представляет собой чисто геометрическую характеристику и называется полярным моментом инерции сечения . Интеграл представляет собой чисто геометрическую характеристику и называется полярным моментом инерции сечения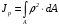 (5.7) (5.7)Т.о., получаем 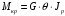 или или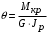 . (5.8) . (5.8)Величину 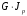 называют жесткостью стержня при кручении. называют жесткостью стержня при кручении.Из (5.8), с учетом (5.4) получим 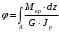 . (5.9) . (5.9)Если Мкр и 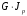 по длине стержня постоянны, то из (5.9) найдем по длине стержня постоянны, то из (5.9) найдем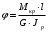 . (5.10) . (5.10)Подставляя (5.8) в (5.6) получим выражение для напряжений  . (5.11) . (5.11)Т.о., касательные напряжения распределены вдоль радиуса по линейному закону и имеют максимальное значение в точках, наиболее удаленных от центра. При этом 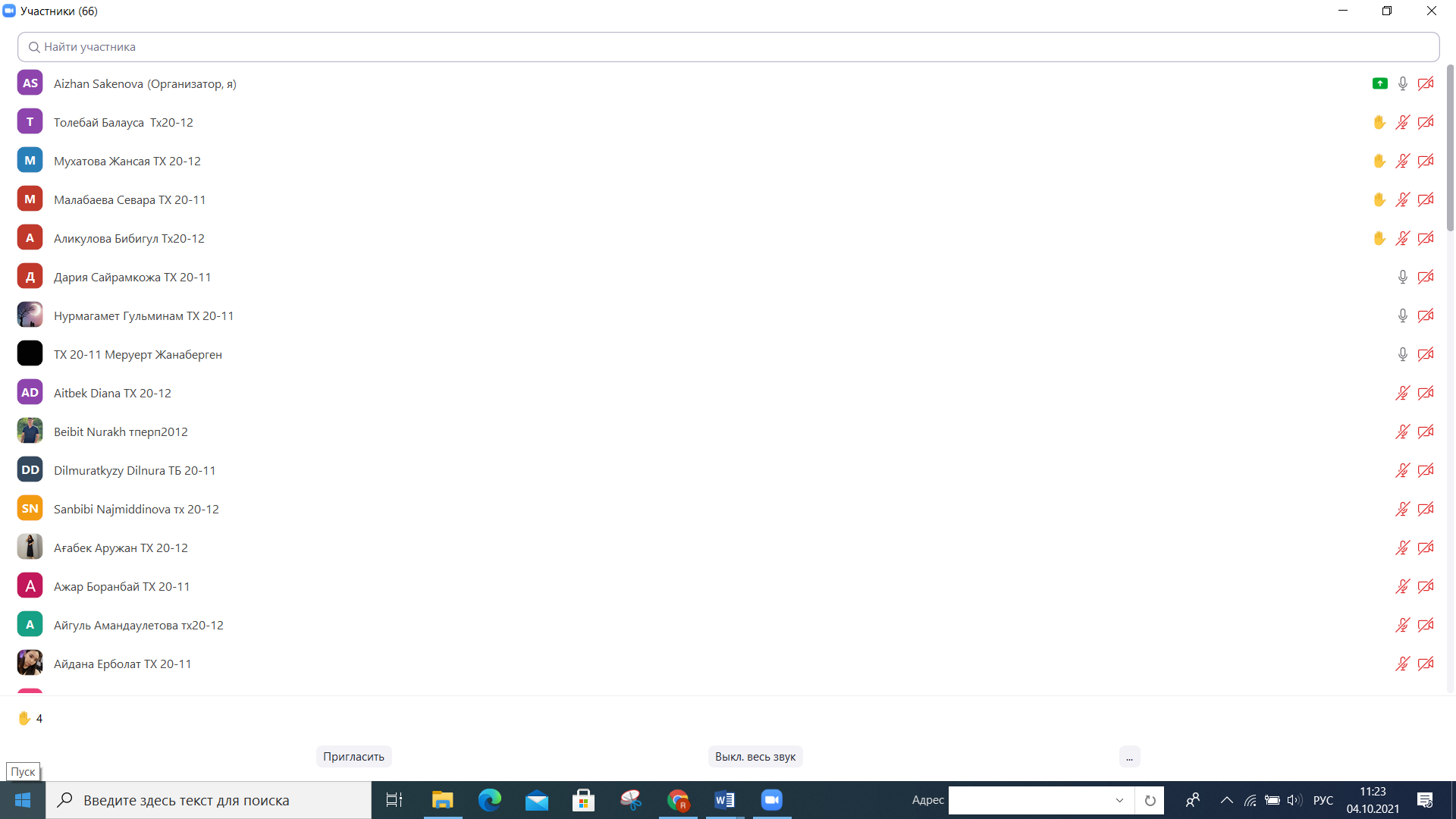 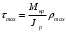 или или 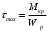 . (5.12) . (5.12)Величина 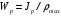 (5.13) (5.13)называется полярным моментом сопротивления поперечного сечения стержня. Формулы (5.10), (5.12) справедливы для кругового и кольцевого сечений. Полярный момент инерции для круглого сечения найдем из (5.7), учитывая, что элементарная площадь пояска dA=2π∙ρ∙dρ (рисунок 5.4). Имеем 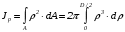 или или 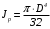 . (5.14) . (5.14)Полярный момент сопротивления для круглого сечения 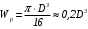 . (5.15) . (5.15)Для кольцевого сечения (с наружным D и внутренним d диаметрами) имеем 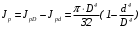 . (5.16) . (5.16)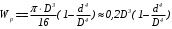 . (5.17) . (5.17)Условие прочности и условие жесткости при кручении имеют вид 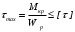 , (5.18) , (5.18)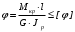 или или 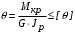 (5.19) (5.19)где [τ], [φ], [θ] – допускаемое касательное напряжение, допускаемый полный и допускаемый относительный углы закручивания соответственно. Пример 5.1 - Для стального стержня кругового сечения (рисунок 5.3) требуется подобрать диаметр из условия прочности при [τ] = 100 МПа, M1=2 кН∙м, M2=3 кН∙м, M3=9 кН∙м, M4=4 кН∙м. Для найденного значения диаметра проверить условие жесткости, если [θ]=3 град/м, модуль сдвига для стали G=8∙104 МПа. Решение. Т.к. поперечное сечение стержня постоянно, опасными будут сечения на втором слева участке, где крутящий момент максимален, Mкр2 = 5 кН∙м. Из условия прочности (12.18) находим 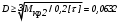 м. Округляя в большую сторону, выбираем окончательно D = 65 мм. м. Округляя в большую сторону, выбираем окончательно D = 65 мм.Определяем момент инерции поперечного сечения Jp=π∙D4/32=1,785∙10-5 м3. Проверяем условие жесткости 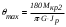 =2,01 град/м < [θ]=3 град/м, т.е. условие жесткости выполняется. =2,01 град/м < [θ]=3 град/м, т.е. условие жесткости выполняется.Геометрические характеристики поперечных сечений. Внутренние силовые факторы при изгибе. Статические моменты и центр тяжести плоской фигуры Рассмотрим некоторую плоскую фигуру в системе координат x, y (рисунок 13.1). Интегралы 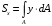 , , 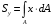 (5.1.1) (5.1.1)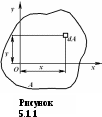 называются статическими моментами фигуры относительно оси x и оси y соответственно. называются статическими моментами фигуры относительно оси x и оси y соответственно.Выясним, как изменяются статические моменты сечения при параллельном переносе координатных осей (рисунок 13.2). Очевидно, что x = x1 - a; y = y1 - b. Тогда 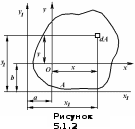 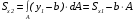 , ,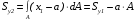 . .Величины а и b можно подобрать (причем единственным образом) так, чтобы статические моменты 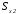 и и 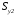 были равны нулю. Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей называется центром тяжести сечения. были равны нулю. Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей называется центром тяжести сечения. В системе координат (x1, y1) координаты центра тяжести равны 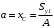 , , 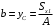 . (5.1.2) . (5.1.2)Отметим, что статический момент составного сечения равен сумме статических моментов составляющих областей. Моменты инерции сечения Возвращаясь к рисунку 5.1.1, рассмотрим три интеграла 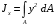 , (5.1.3) , (5.1.3)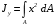 , (5.1.4) , (5.1.4)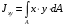 . (5.1.5) . (5.1.5)Первые два интеграла называются осевыми моментами инерции относительно осей x и y соответственно, третий центробежным моментом инерции сечения относительно осей x, y. Осевые моменты всегда положительны, центробежный может быть как положительным, так и отрицательным. При параллельном переносе координатных осей (рисунок 5.1.2) моменты инерции изменяются в соответствии с формулами 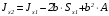 , (5.1.6) , (5.1.6)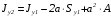 , (5.1.7) , (5.1.7)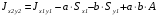 . (5.1.8) . (5.1.8)Если x1 и y1 - центральные, то 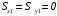 и и 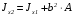 , (5.1.9) , (5.1.9)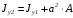 , (5.1.10) , (5.1.10)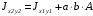 . (5.1.11) . (5.1.11)Т.о., при параллельном переносе осей в случае, когда одна из осей – центральная, осевые моменты инерции изменяются на величину, равную произведению площади на квадрат расстояния между осями. При этом в семействе параллельных осей момент инерции относительно центральной оси минимален. 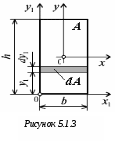 Пример 13.1 - Определить осевые моменты инерции прямоугольника относительно осей x1, y1 и x, y (рисунок 5.1.3). Пример 13.1 - Определить осевые моменты инерции прямоугольника относительно осей x1, y1 и x, y (рисунок 5.1.3). Решение. В качестве элементарной площадки dA возьмем полоску шириной b и высотой dy. Тогда 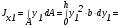 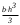 . .По формуле (5.1.9) получаем 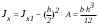 . (5.1.12) . (5.1.12)Аналогично получаем 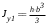 , , 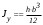 . Центробежный момент инерции . Центробежный момент инерции 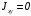 ввиду того, что оси x и y являются осями симметрии, а относительно осей x1 и y1 равен ввиду того, что оси x и y являются осями симметрии, а относительно осей x1 и y1 равен 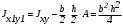 . .Отметим, что моменты инерции составного сечения равны суммам моментов инерции составляющих областей. Главные оси и главные моменты инерции Рассмотрим, как изменяются моменты инерции плоского сечения при повороте осей координат из положения x и y к положению u и v. Из рисунка 13.4 легко установить, что u = y∙ sin + x ∙ cos ; v = y∙ cos x∙ sin . (5.1.13) Из выражений 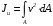 , , 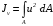 , , 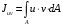 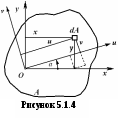 с учетом (13.13) после несложных преобразований получим с учетом (13.13) после несложных преобразований получим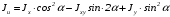 , (5.1.14) , (5.1.14)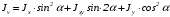 , (5.1.15) , (5.1.15)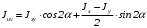 . (5.1.16) . (5.1.16)Складывая первые два уравнения, получаем 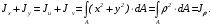 (5.1.17) (5.1.17)Т.о., сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей при повороте осей постоянна и равна полярному моменту инерции плоской фигуры. С помощью (5.1.17) несложно определить осевой момент инерции кругового сечения относительно диаметра. Т.к. 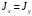 ввиду симметрии, то ввиду симметрии, то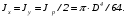 (5.1.18) (5.1.18)Т.к. с изменением угла значения 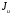 и и 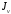 . изменяются, а их сумма остается постоянной, то существует такое значение =0, при котором один из моментов . изменяются, а их сумма остается постоянной, то существует такое значение =0, при котором один из моментов 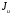 или или 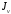 достигает своего максимального значения, другой – минимального. Значение 0 найдем, исследуя на экстремум достигает своего максимального значения, другой – минимального. Значение 0 найдем, исследуя на экстремум 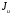 или или 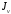 . Найдем . Найдем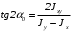 . (5.1.19) . (5.1.19)Оказывается, что при =0 одновременно центробежный момент инерции 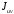 обращается в нуль. Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения, называются главными осями инерции. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Они определяются с использованием (13.14), (13.15) и (13.19) как обращается в нуль. Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения, называются главными осями инерции. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Они определяются с использованием (13.14), (13.15) и (13.19) как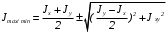 . (5.1.20) . (5.1.20)Радиусом инерции плоской фигуры относительно какой-либо оси l называют величину, определяемую как 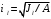 . (5.1.21) . (5.1.21)1. Вопросы для текущего контроля: 1. При каком нагружении возникает кручение бруса (вала)? 2. Как вычисляют значение крутящего момента в поперечном сечении вала? С какой целью строят эпюры крутящих моментов? 3. Какие допущения положены в основу вывода формулы для касательных напряжений возникающих в поперечном сечении вала при кручении? 4. Какое напряженное состояние возникает в каждой точке бруса круглого сечения при кручении? 5. Как составляется условие прочности и условие жесткости для валов при кручении? |
