Домоводство. Решение Разделим брус на участки, границы которых определяются местами изменения поперечных размеров бруса и точками приложения внешних нагрузок
 Скачать 1.14 Mb. Скачать 1.14 Mb.
|
|
Здравствуйте! Решила сама сделать контрольную по техмеху. В этом документе на стр.2-12 решенная мной контрольная, на стр.13-30 та же контрольная, но переписанная в тетрадь, и с замечаниями преподавателя. Нужно сделать работу над ошибками. Задача 6Для заданного бруса построить эпюры продольных сил и нормальных напряжений в поперечном сечении бруса на каждом участке, приняв [σ]р = 160 МПа, [σ]с = 120 МПа, а также определить удлинение (укорочение) бруса, если модуль продольной упругости Е = 2105 МПа. Вес бруса не учитывать. Дано: F1 = 26 кН, F2 = 46 кН, А1 = 2,2 см2, А2 = 1,7 см2, l1 = 150 мм; l2 = 110 мм; l3 = 140 мм, Е = 2105 МПа, [σ]р = 160 МПа, [σ]с = 120 МПа. Определить: l Решение: Разделим брус на участки, границы которых определяются местами изменения поперечных размеров бруса и точками приложения внешних нагрузок. Рассматриваемый брус имеет три участка. Для закрепленного одним концом бруса расчет целесообразно вести со свободного конца, чтобы не определять опорной реакции. Применяя метод сечений, определяем продольную силу N, выражая ее через внешние силы F1 и F2. Проводя в пределах каждого из участков сечение, будем отбрасывать левую закрепленную часть бруса и оставлять для рассмотрения правую часть. На участке I продольная сила равна На участке II продольная сила равна Положительное значение N показывает, что на участках I и II брус растянут. На участке III сила равна Знак «минус» показывает, что брус на III участке сжат. По полученным из расчета данным строим эпюру N. Для этого параллельно оси бруса проведем базовую (нулевую) линию эпюры, откладываем перпендикулярно ей в произвольном масштабе полученные значения N. В пределах каждого участка нагружения продольная сила постоянная, а потому на эпюре изобразится прямой, параллельной базовой. Положительные значения будем откладывать вверх от базовой линии, а отрицательные – вниз. Эпюра штрихуется линиями, перпендикулярными оси бруса. Эпюра продольных сил представляет собой график, выражающий закон изменения продольной силы во всей длине бруса. Любая ордината эпюры продольных сил, измеренная в соответствующем масштабе, выражает величину продольной силы в данном поперечном сечении. Дня определения напряжений σ в любом поперечном сечении значение продольной силы, действующей в данном сечении необходимо разделить на площадь этого сечения: Находим напряжения на каждом участке бруса и строим эпюру: В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений. При построении эпюр и проверке их правильности руководствуемся следующими правилами: 1) Скачки на эпюрах N имеют место в точках приложения сосредоточенных сил. Величина скачка равна внешней силе, приложенной в этом сечении. 2) На эпюре σ скачки имеют место не только в точках приложения сосредоточенных сил, но и в местах изменения площади поперечного сечения. 3) Знаки на участках эпюры σ должны совпадать со знаками на соответствующих участках эпюры N. Выполняем проверку прочности бруса, т.е. расчетное напряжение (для каждого участка в отдельности) сравниваем с допускаемыми: На участке I имеет место небольшая недогрузка 1,5%. Но величины превышений от допускаемых напряжений в пределах 5% в реальном проектировании считаются возможными. На участке II перегрузка составляет 27,4%. На участке III недогрузка составляет 26,5%. Это говорит о том, что сечение на участках II и III выбрано неэкономично, имеет место большой перерасход материала. Полное удлинение бруса равно алгебраической сумме удлинений его участков: Определим Полученный в ответе знак «плюс» говорит о том, что в целом брус удлинился, т.е. свободный конец переместился в нашем случае вправо. 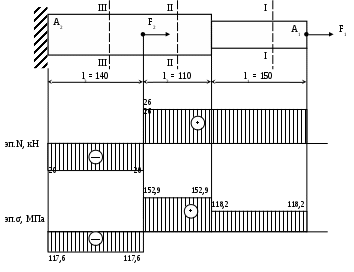 Задача 26Для заданной консольной балки построить эпюры поперечных сил и изгибающих моментов. Подобрать сечение балки в виде двутавра, если [σ] = 160 МПа. Дано: F = 22 кН, q = 8 кН/м, М = 20 кНм, l1 = 2 м; l2 = 2 м; [σ] = 160 МПа. Определить: сечение балки Решение: 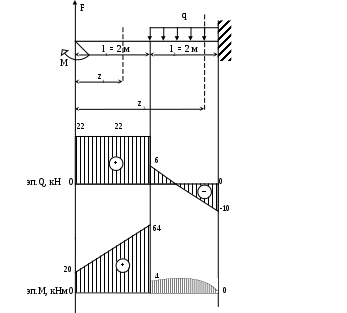 Разбиваем балку на участки. Границы участков целесообразно проводить через точки приложения сосредоточенных сил, моментов, начала и конца равномерно распределенной нагрузки. Построение эпюр Q и Мu будем вести от свободного конца, чтобы не определять реакции опор. Для того чтобы вычислить поперечную силу и изгибающий момент в произвольном сечении, необходимо мысленно рассечь плоскостью в этом месте балку и правую часть балки отбросить. Затем по действующим на оставленную часть балки внешним силам надо найти искомые значения Qy и Мx, причем знак их надо определить по тому действию, какое оказывают внешние силы на оставленную часть балки в соответствии с принятым ранее правилом знаков. Построение эпюры поперечных сил. Проводим сечение I-I Так как поперечная сила в пределах первого участка является величиной постоянной, поэтому эпюра Q на участке I представляется прямой, параллельной базовой линии. Проводим сечение II-II Так как Q2=f(z2) является уравнением прямой линии, для ее построения нужны две точки: при z = 2 Q = 6 кН при z = 4 Q = – 10 кН Проводим базовую линию эпюры Q, перпендикулярной к ней откладываем ординаты, соответствующие z = 2 и z = 4. Построение эпюры изгибающих моментов. Сечение I-I при z = 0 М = 20 кНм при z = 2 М = 64 кНм Сечение II-II 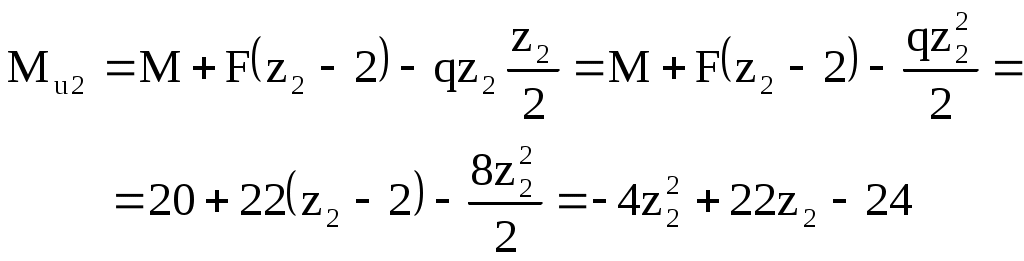 Зависимость Mu(z2) изображается графически квадратной параболой. Для построения параболы нужны как минимум три точки: при z = 2 М = 4 кНм при z = 3 М = 6 кНм при z = 4 М = 0 кНм Проводим базовую линию эпюры и откладываем ее ординаты, соответствующие значениям z =2, z = 3, z = 4 м. Соединяем точки, получаем квадратную параболу, направленную выпуклостью навстречу нагрузке Подбираем номер профиля двутавра из условия прочности при изгибе, если [σ]u = 160 МПа. Отсюда: По значению Wx = 400 см3 подходит двутавровый профиль №30, для которого Wx = 472 см3. Задача 36Для двухопорной балки построить эпюры поперечных сил и изгибающих моментов. Подобрать сечение балки, составленной из двух швеллеров, если [σ] = 160 МПа. Дано: F1 = 65 кН, F2 = 10 кН, М = 35 кНм, l1 = 4 м; l2 = 4 м; l3 = 2 м; l4 = 4 м; [σ] = 160 МПа. Определить: сечение балки 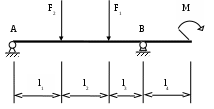 Решение: Расчет балки, опирающейся на две шарнирные опоры, следует начать с определения опорных реакций, исходя из условия ее равновесия. Определим опорные реакции Составим уравнение моментов относительно опор А и В: или или Для проверки составим сумму проекций всех сил на вертикальную ось: Построение эпюры поперечных сил. Проводим сечение I-I Сечение II-II Сечение III-III Сечение VI-VI Построение эпюры изгибающих моментов. Сечение I-I при z = 0 М = 0 при z = 4 М = 90 кНм Сечение II-II при z = 4 М = 90 кНм при z = 8 М = 140 кНм Сечение III-III при z = 8 М = 140 кНм при z = 10 М = 35 кНм Сечение VI-VI Рассматривая часть балки, расположенную справа от сечения, получим 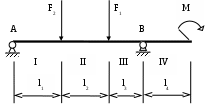 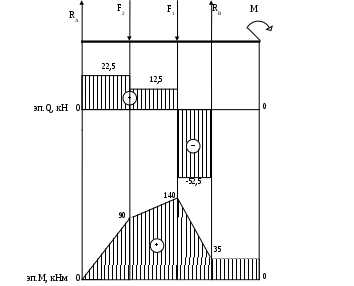 Подбор сечения осуществляется из условия прочности. Момент сопротивления всего сечения Момент сопротивления одного швеллера По вычисленному значению выбираем швеллер №33, для которого Wx = 484 см3. При этом в сечении А балки возникнут напряжения что не превышает значение [σ].                 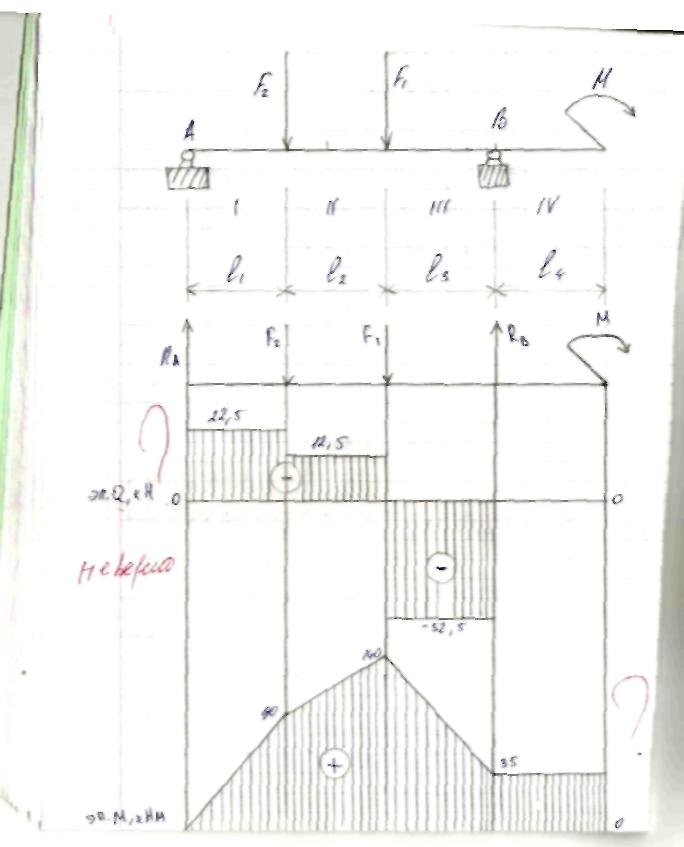  |
