Задание1 вар.15. Решение с учётом исходных данных, при постоянном ускорении зависимость скорости от времени имеет вид
 Скачать 194.28 Kb. Скачать 194.28 Kb.
|
 Задача №1 (вариант 15) Частица движется равноускорено в координатной плоскости XY с начальной скоростью 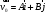 и ускорением и ускорением 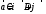 . Найти модули векторов скорости v , тангенциального а и нормального аn ускорений, а также радиус кривизны траектории R в момент времени t. . Найти модули векторов скорости v , тангенциального а и нормального аn ускорений, а также радиус кривизны траектории R в момент времени t.Дано: 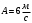 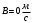 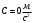 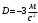 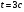 Найти: 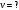 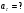 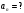 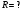 Решение: С учётом исходных данных 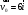 , ,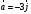 при постоянном ускорении зависимость скорости от времени имеет вид: 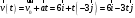 Откуда модуль вектора скорости равен 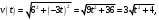 модуль тангенциального ускорения составит: 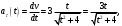 модуль полного ускорения постоянен и равен: 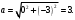 Так как 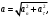 то модуль нормального ускорения равен то модуль нормального ускорения равен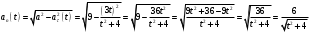 В частности, для момента времени t=3 c имеем 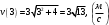 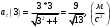 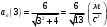 Наконец, поскольку нормальное ускорение тела, движущегося со скоростью v по траектории с радиусом кривизны R равно 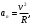 то то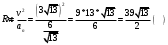 Ответ: 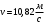 , , 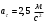 , , 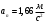 , , 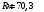 . .Задача №2 (вариант 15) 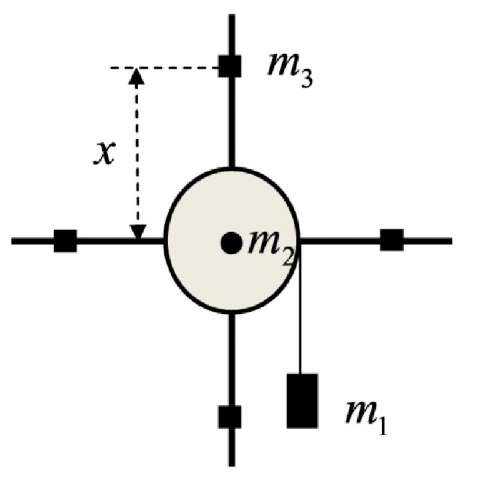 На однородный цилиндрический блок массой m2 и радиусом R намотана невесомая нить, к свободному концу которой прикреплен груз массой m1. К блоку крестообразно прикреплены четыре одинаковых невесомых стержня, на которых закреплены одинаковые грузы массой m3 на расстоянии x от оси вращения. Грузы m3 можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения a груза m1 от расстояния x. Построить график этой зависимости в интервале изменения x от R до 3R. Ускорение свободного падения g=9,81 м/с2. Дано: 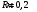 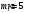 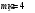 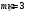 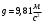 Найти: 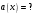 Решение: Зададим систему отсчета. За начало отсчета принимаем поверхность земли, ось x направим вертикально вниз. По закону сохранения полной механической энергии, уменьшение потенциальной энергии груза m1 идет на увеличение кинетической энергии груза m1, вращательной кинетической энергии блока m2 и четырех грузов m3 закрепленных на стержнях. Следовательно, можно составить следующее уравнение: 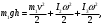 (1) (1)где 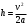 - расстояние которое проходит груз m1, - расстояние которое проходит груз m1,  - его скорость, - его скорость, 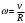 - угловая скорость блока, - угловая скорость блока, 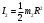 - момент инерции блока относительно оси вращения, - момент инерции блока относительно оси вращения, 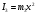 - момент инерции одного груза закрепленного на стержне относительно оси вращения. - момент инерции одного груза закрепленного на стержне относительно оси вращения.В итоге уравнение (1) примет следующий вид: 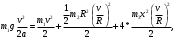 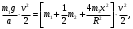 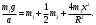 (2) (2)В итоге из уравнения (2) выразим ускорение: 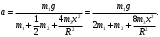 (3) (3)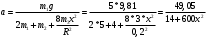 Построим график a(x) в интервале измененияx от0,2 до0,6 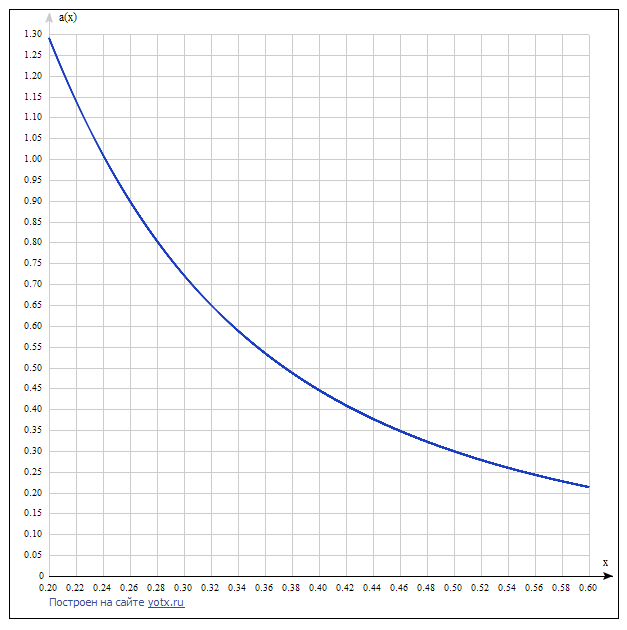 Ответ: 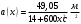 . .Задача №3 (вариант 15) Шар массой m1, летящий со скоростью v1, сталкивается с неподвижным шаром массой m2. После удара шары разлетаются под углом друг к другу. Удар абсолютно упругий, столкновение происходит в горизонтальной плоскости. Найти скорости шаров и1 и u2 после удара. Дано: 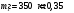 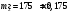 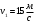 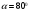 Найти: 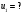 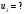 Решение:  Обозначим начальный и конечные импульсы тел: 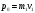 - первого шара до удара; - первого шара до удара;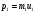 , - первого шара после удара; , - первого шара после удара;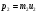 - второго шара после удара. - второго шара после удара.Тогда из треугольника импульсов в соответствии с законом сохранения импульса и законом сохранения механической энергии получим следующую систему уравнений 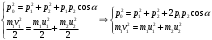 Для удобства дальнейших преобразований заменим 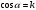 и тогда получим и тогда получим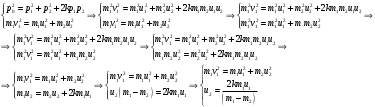 Решим первое уравнение подставив в него значение второго уравнения 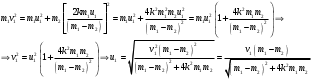 Теперь подставим это выражение во второе уравнение системы 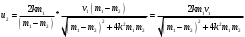 В итоге заменив обратно 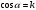 получим в итоге получим в итоге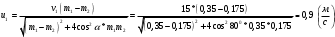 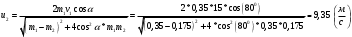 Ответ: 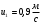 , , 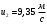 . . |
