Эконометрика. Решение Система нормальных уравнений
 Скачать 30.71 Kb. Скачать 30.71 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Эконометрика Группа Го19Э271 Студент А.В. Голубцова МОСКВА 2021 Задачи: Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3 Таблица 3. Регрессионный анализ.
Решение: Система нормальных уравнений. 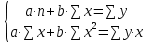  Линейная зависимость Для расчета параметров регрессии построим расчетную таблицу
Для наших данных система уравнений имеет вид   Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения. Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения.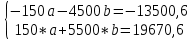 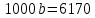 Откуда Откуда 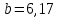 Найдем Найдем 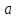 : :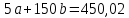 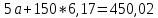  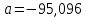 Уравнение линейной регрессии: Уравнение линейной регрессии: Экспоненциальная зависимость
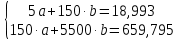 Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения. Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения.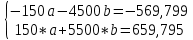 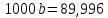 Откуда Откуда  Найдем 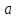 : : 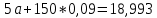 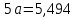  Уравнение экспоненциальной зависимости: y = e1,099e0,09x = 3,00046e0,09x Уравнение экспоненциальной зависимости: y = e1,099e0,09x = 3,00046e0,09xСтепенная зависимость Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
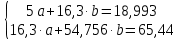 Домножим 1-е уравнение системы на (-3,26), получим систему, которую решим методом алгебраического сложения, Домножим 1-е уравнение системы на (-3,26), получим систему, которую решим методом алгебраического сложения,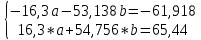 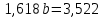 Откуда Откуда 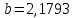 Найдем 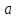 : :   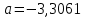 Уравнение степенной зависимости: y = e-3,3060x2,1793 = 0,03666x2,1793 Уравнение степенной зависимости: y = e-3,3060x2,1793 = 0,03666x2,1793Логарифмическая зависимость Для расчета параметров регрессии построим расчетную таблицу (табл, 1)
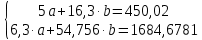 Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения. Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения.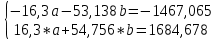 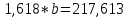 Откуда Откуда 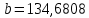 Найдем Найдем 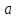 : :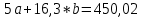 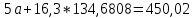 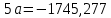  Уравнение логарифмической зависимости: Уравнение логарифмической зависимости: 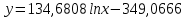 Показательная зависимость
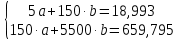 Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения. Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения.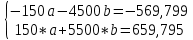 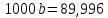 Откуда Откуда  Найдем 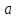 : : 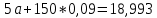 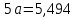  Уравнение показательной зависимости: y = e1,0988*e0,09x = 3,00046*1,09417x Уравнение показательной зависимости: y = e1,0988*e0,09x = 3,00046*1,09417xВычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4. Таблица 4. Корреляционный анализ.
Решение: Для расчета параметров регрессии построим расчетную таблицу
Выборочные средние: 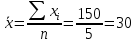 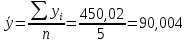  Выборочные дисперсии: Выборочные дисперсии: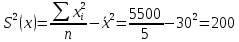 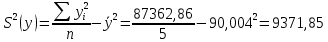 Среднеквадратическое отклонение: 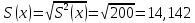 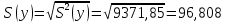 Рассчитываем количественное значение коэффициента парной линейной корреляции по формуле: 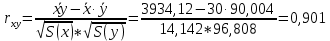 По шкале Чеддока модуль коэффициента парной линейной корреляции расположен в числовом интервале 0,9 – 1, значит, связь между х и у весьма высокая и прямая. |
