контрольная по математике. kontrolnaya Математика. Решение. Так как, то получим
 Скачать 226 Kb. Скачать 226 Kb.
|
МОСКВА 2020 1. Метод изоклин построить интегральные кривые уравнения. Решение. Так как При При При При При При При 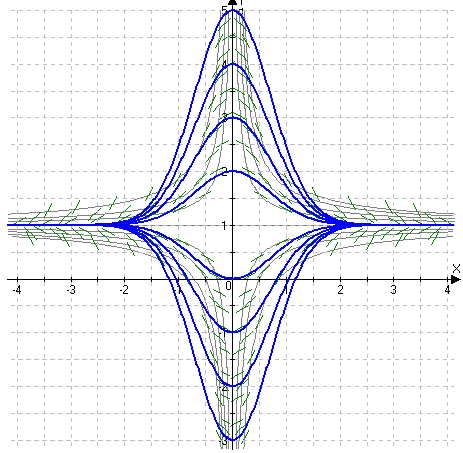 2. Решить уравнение допускающее понижение порядка. Решение. Замена Сделаем обратную замену, получим уравнение 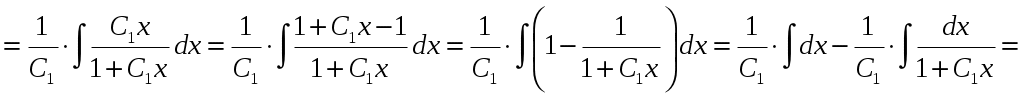 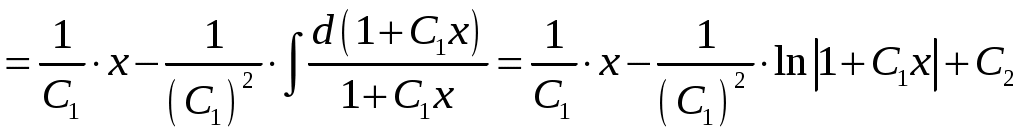 . .Ответ: 3. Решить систему уравнений 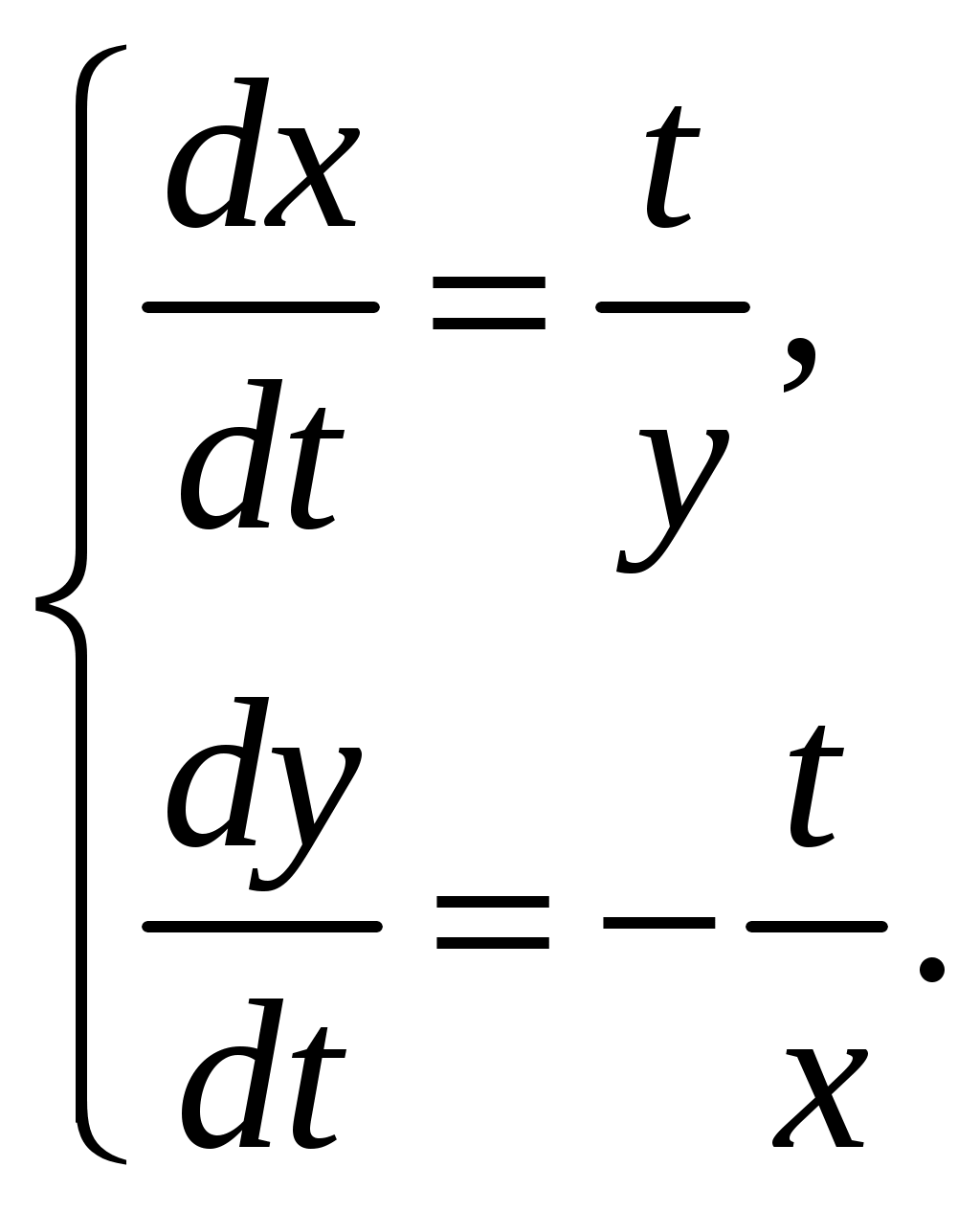 Решение. Из 1-го уравнения системы Подставим Дифференцируем функцию 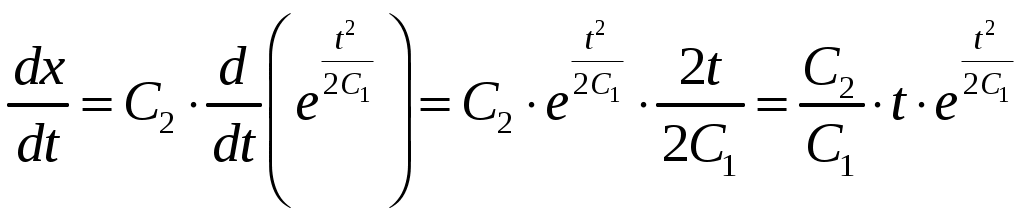 . Подставим . Подставим 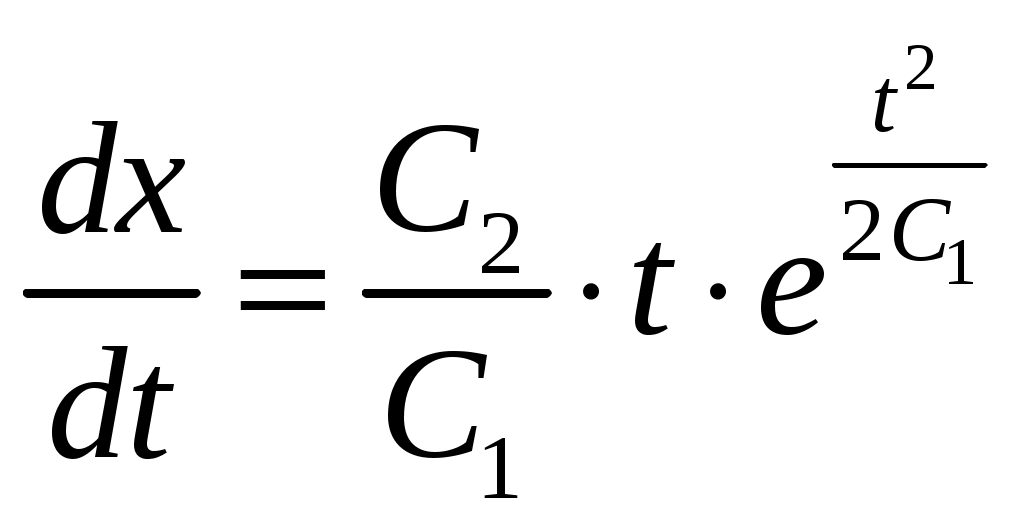 в 1-ое уравнение системы в 1-ое уравнение системы 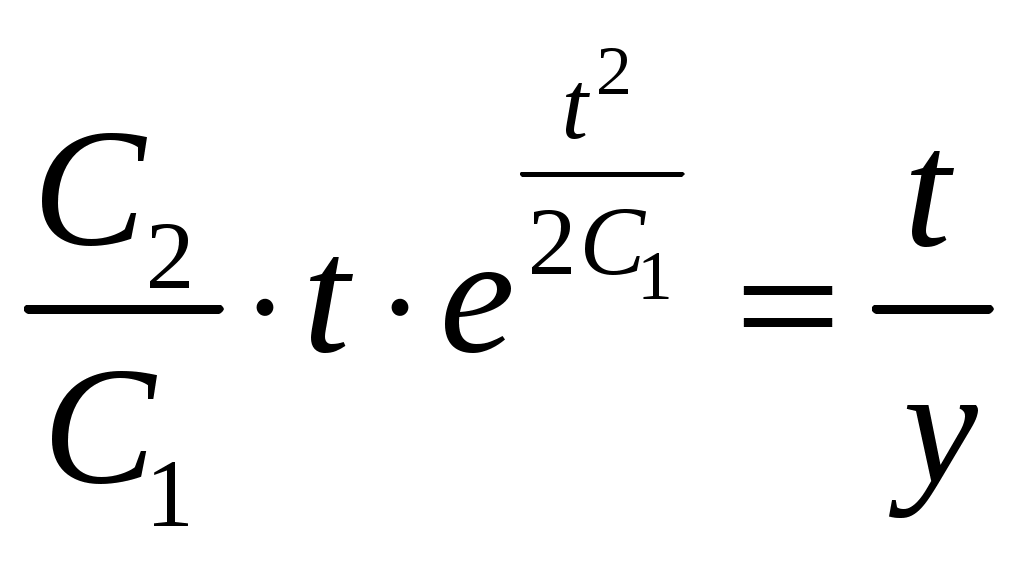 , , 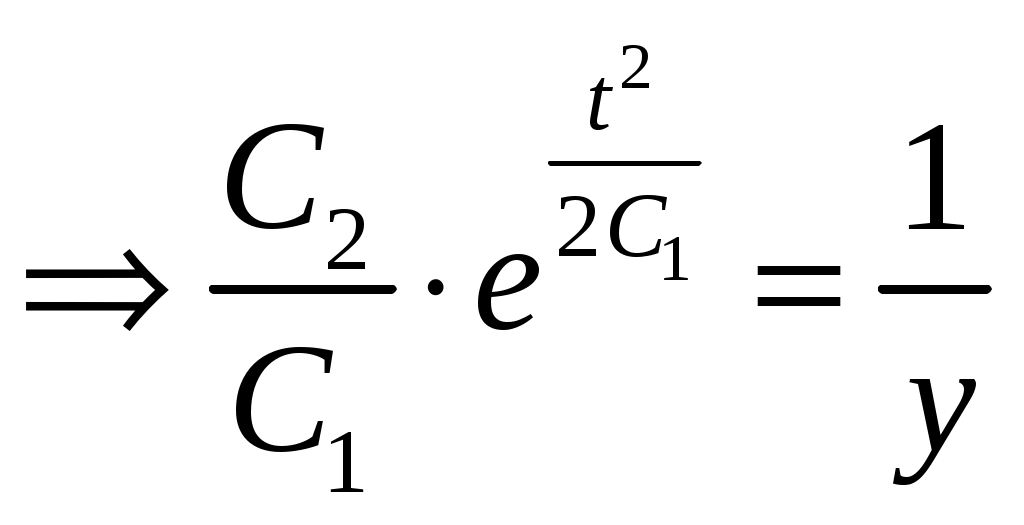 , , 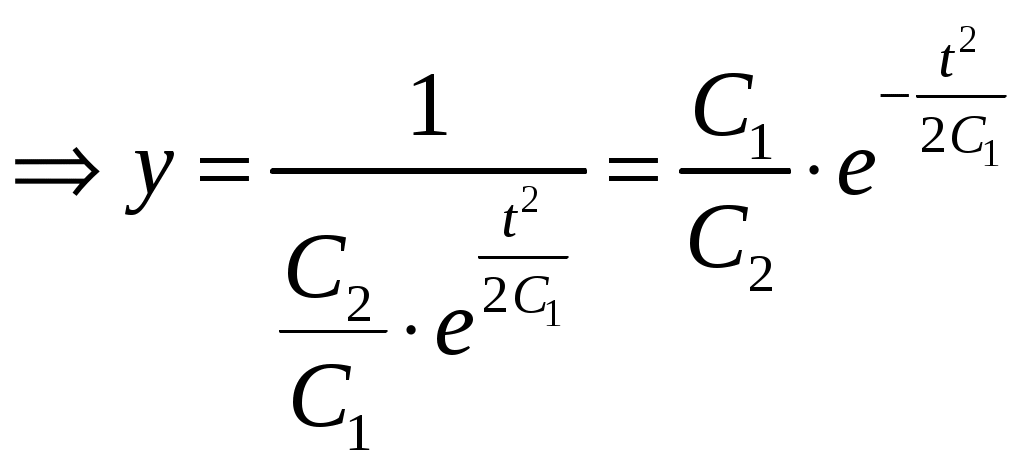 . .Общее решение системы равно 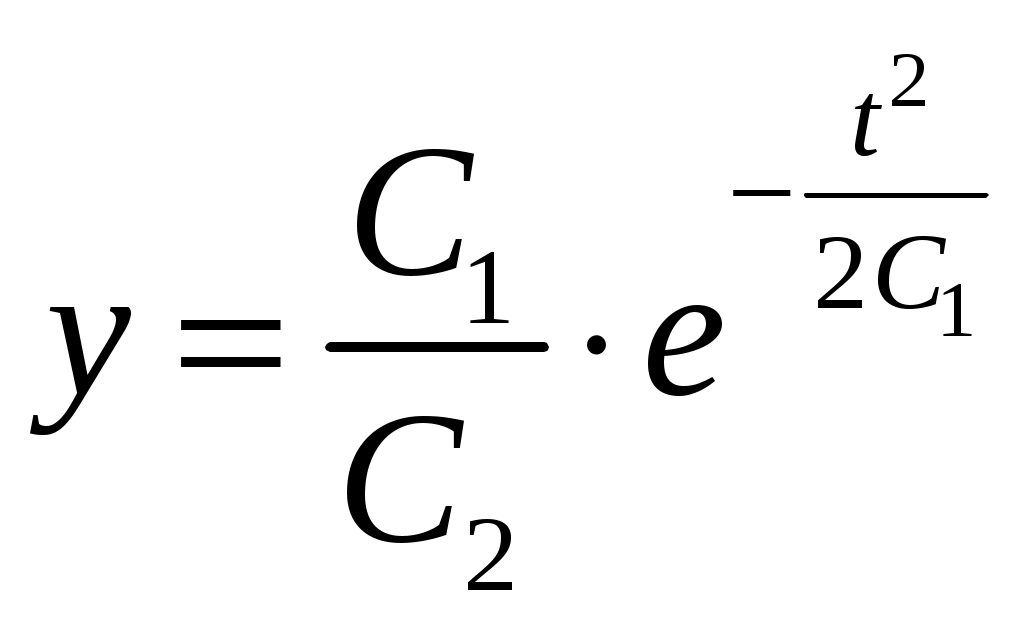 . .Ответ: 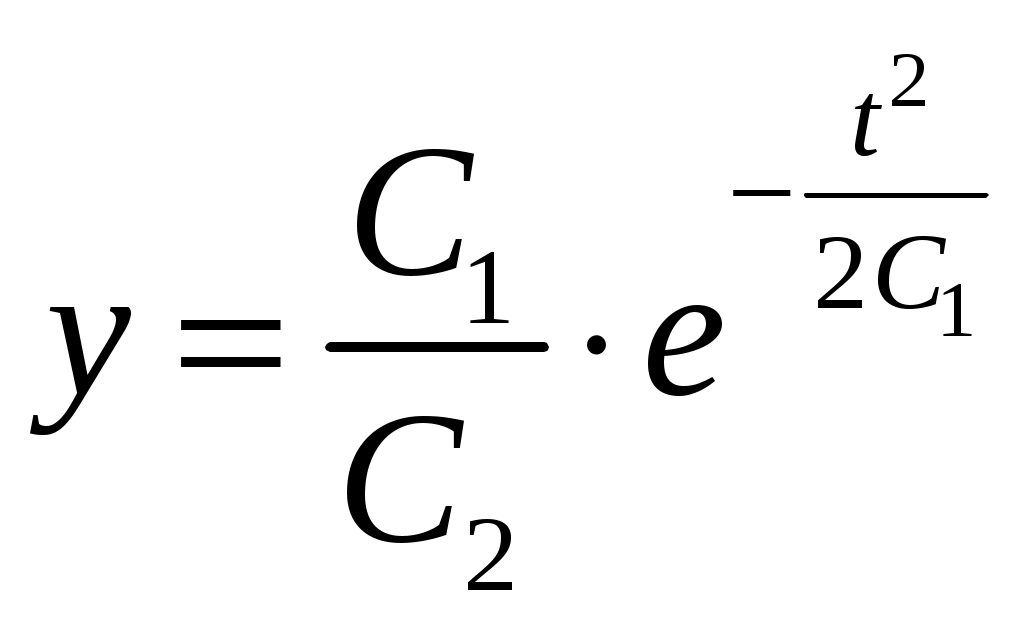 . .4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Решение. По условии задачи имеем 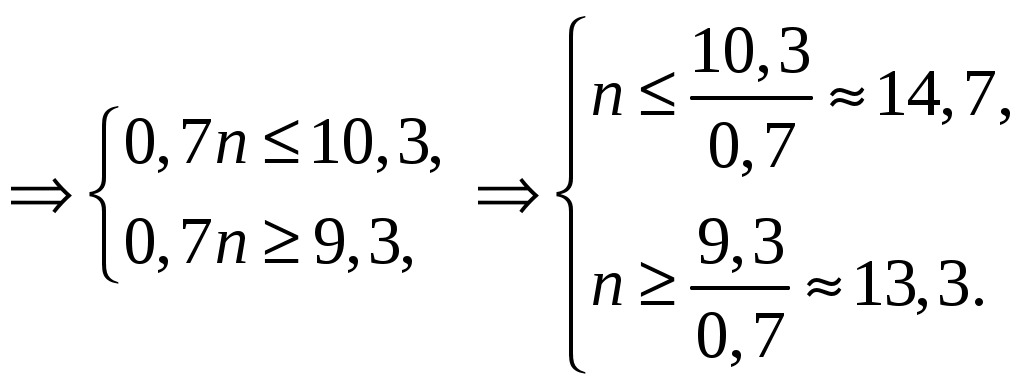 . Число испытаний равно . Число испытаний равно Ответ: 14. | ||||||||||||||||||||||||||
