АСУ на транспорте. 27_АСУ. Решение транспортной задачи в информационной среде MicrosoftExcel По дисциплине
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ» Кафедра транспорта и логистики Решение транспортной задачи в информационной среде MicrosoftExcel По дисциплине Автоматизированные системы управления на транспорте Выполнила: ст. гр. ЗТЖ-192 Гончарова М.А. Проверил: преподаватель Медведева К.С. Н  овокузнецк овокузнецк 2021 Исходные данные: 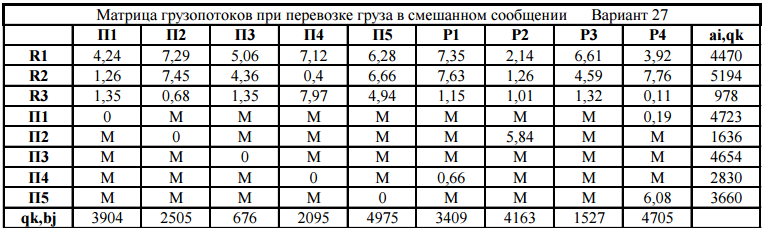 Решение задачи: 1. Настраиваю лист Microsoft Excel. 1.1 Нажимаю на ленте вкладку "Файл", выбираю диалоговое окно Параметры, во вкладке "Формулы" активирую итерационные вычисления и устанавливаю предельное количество итераций равное – 1000 [Рисунок 1]. 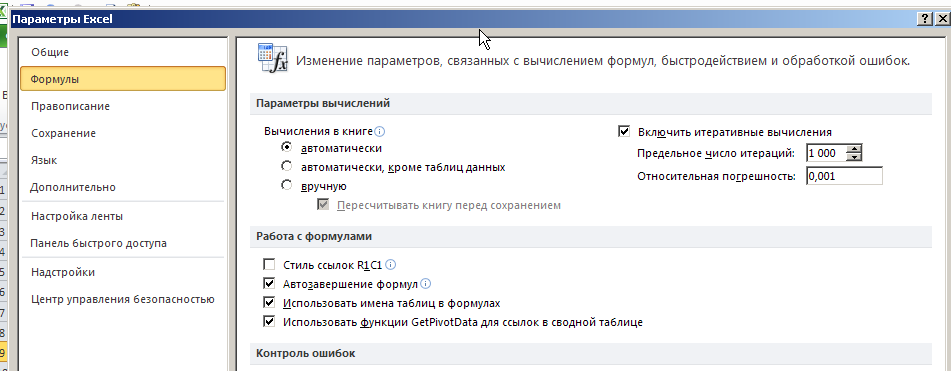 Рисунок 1 - Результат открытия вкладки «Формулы» в диалоговом окне «Параметры», а также результат включения итеративного вычисления и установки предельного числа итераций во вкладке «Параметры вычисления» 1.2 Через диалоговое окно Параметры Excel, во вкладке «Надстройки» включаем функцию "Поиск решений" [Рисунок 2]. 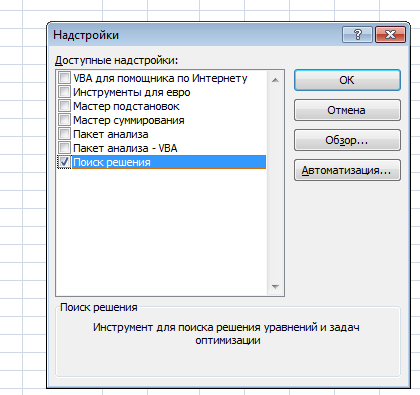 Рисунок 2 – Результат включения функции «Поиск решения» в диалоговом окне «Надстройки» листа Microsoft Excel. 2. Порядок решения 2.1 Заносим на лист Microsoft Excel матрицу с исходными данными [Рисунок 3]. 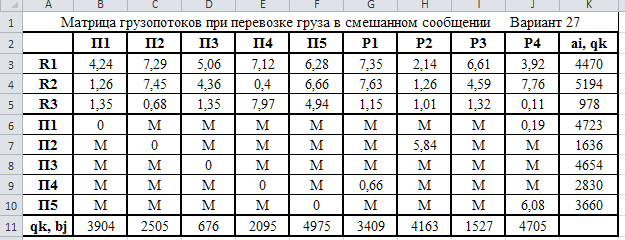 Рисунок 3 – Результат ввода исходной матрицы на лист Microsoft Excel 2.2 Добавляем в исходную матрицу строку для фиктивного поставщика (в качестве показателей оптимальность ставим «0» или запрет «М») [Рисунок 4]. 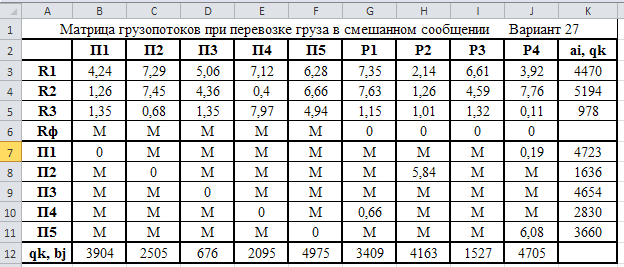 Рисунок 4 – Результат ввода фиктивного поставщика 2.3 Добавляем в исходную матрицу столбец для фиктивного потребителя (в качестве показателей оптимальность ставим «0» или запрет «М») [Рисунок 5]. 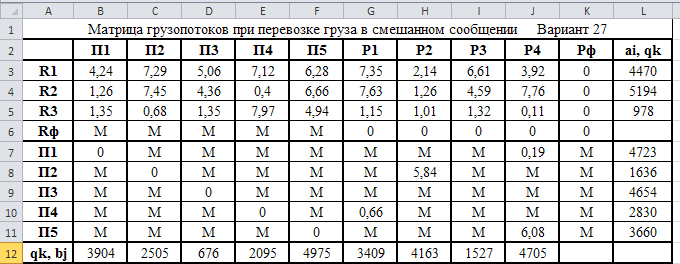 Рисунок 5 – Результат ввода фиктивного потребителя 2.4 При помощи оператора «ЕСЛИ» определяем значения потребности фиктивного потребителя и ресурсы фиктивного поставщика [Рисунки 6 - 8]. 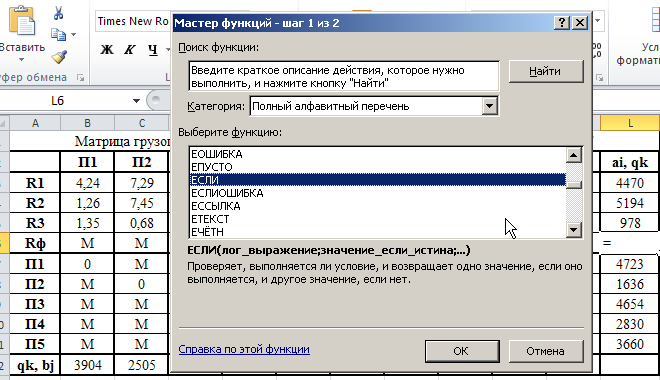 Рисунок 6 – Результат открытия в строке формул мастера функций оператора «ЕСЛИ» 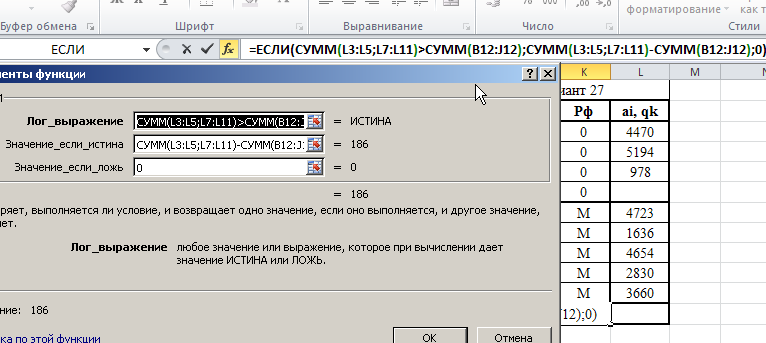 Рисунок 7 – Ввод функции определяющей потребность фиктивного потребителя 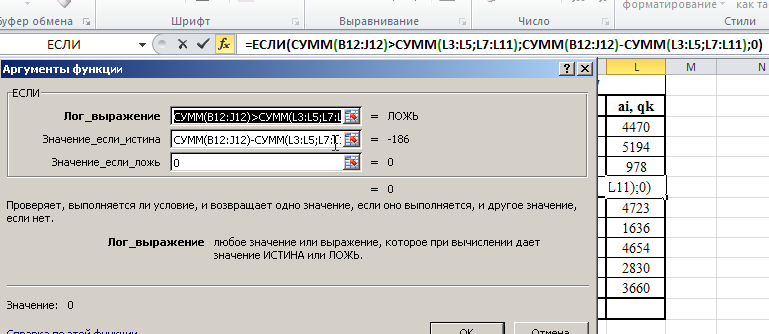 Рисунок 8 – Ввод функции определяющей ресурсы фиктивного поставщика 2.5 При помощи оператора «ЕСЛИ» проверяем правильность занесения в матрицу корреспонденций фиктивных участников перевозок [Рисунок 9]. 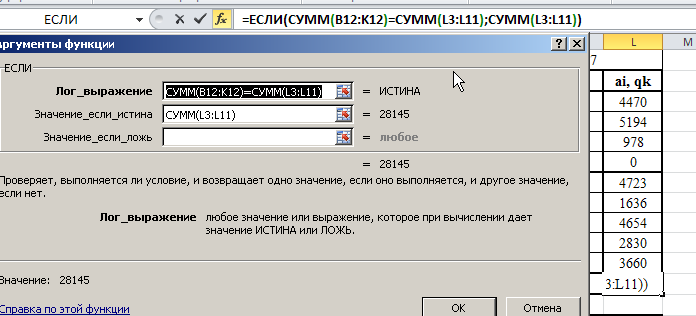 Рисунок 9 – Ввод функции определяющей правильность ввода параметров фиктивных участников перевозок 2.6 Выделяем и копируем исходную матрицу [Рисунок 10]. 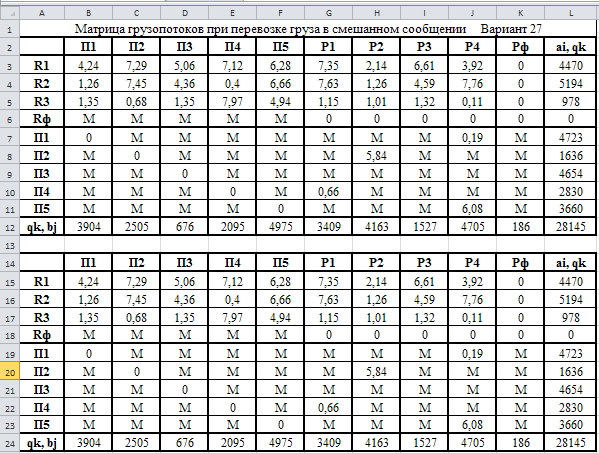 Рисунок 10 – Результат копирования исходной матрицы 2.7 Удаляем в матрице №2 всё кроме запретов - М [Рисунок 11]. 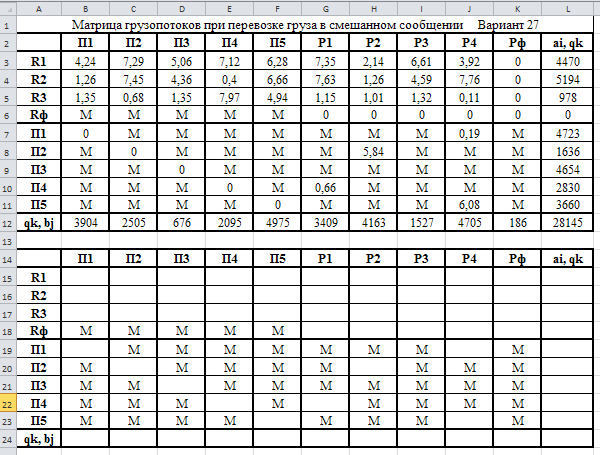 Рисунок 11 – Результат преобразования матрицы №2 2.8 В качестве корреспонденций в рабочем поле матрицы №2 вводим - 1 [Рисунок 12]. 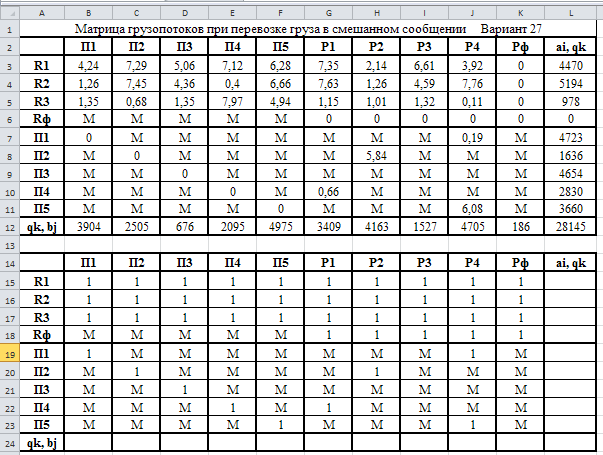 Рисунок 12 – Результат ввода корреспонденций в матрице №2 2.9 При помощи оператора «СУММ» определяем: 2.9.1 Суммы корреспонденций в каждой строке второй матрицы [Рисунок 13]. 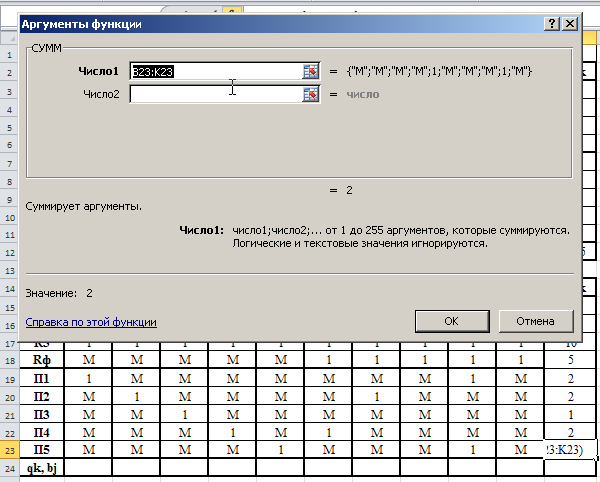 Рисунок 13 – Определение суммарных корреспонденций строк второй матрицы 2.9.2 суммы корреспонденций в каждом столбце второй матрицы [Рисунок 14]. 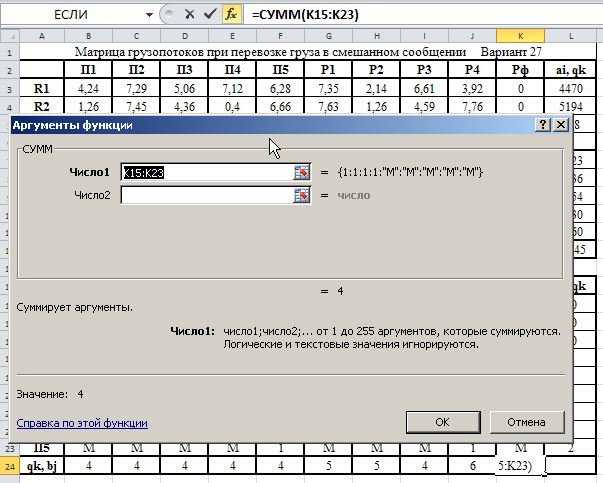 Рисунок 14 – Определение суммарных корреспонденций столбцов второй матрицы 2.10 При помощи оператора «СУММПРОИЗВ» вводим целевую функцию [Рисунок 15]. 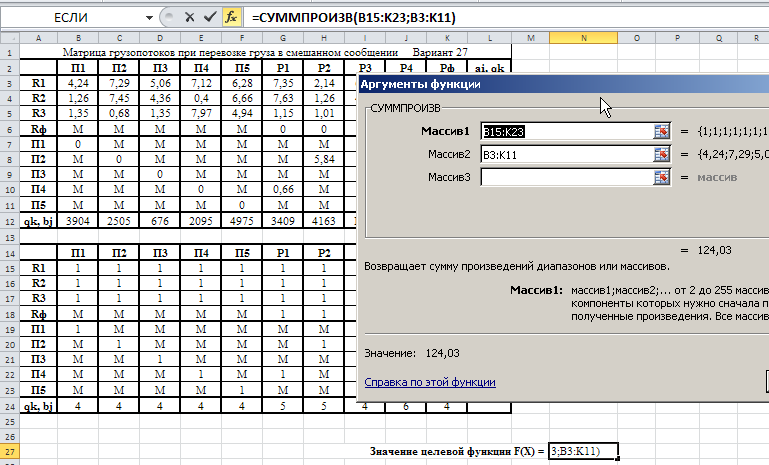 Рисунок 15 – Ввод целевой функции 2.11 Открытие приложения «Поиск решения» [Рисунки 16 - 17]. 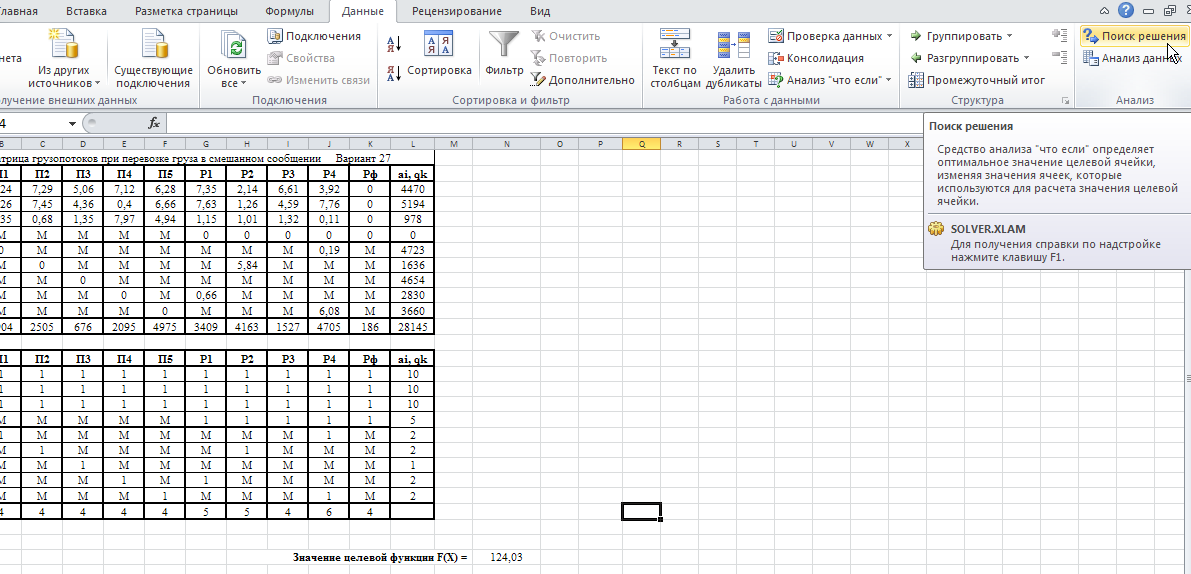 Рисунок 16 – Открытие приложения «Поиск решения» 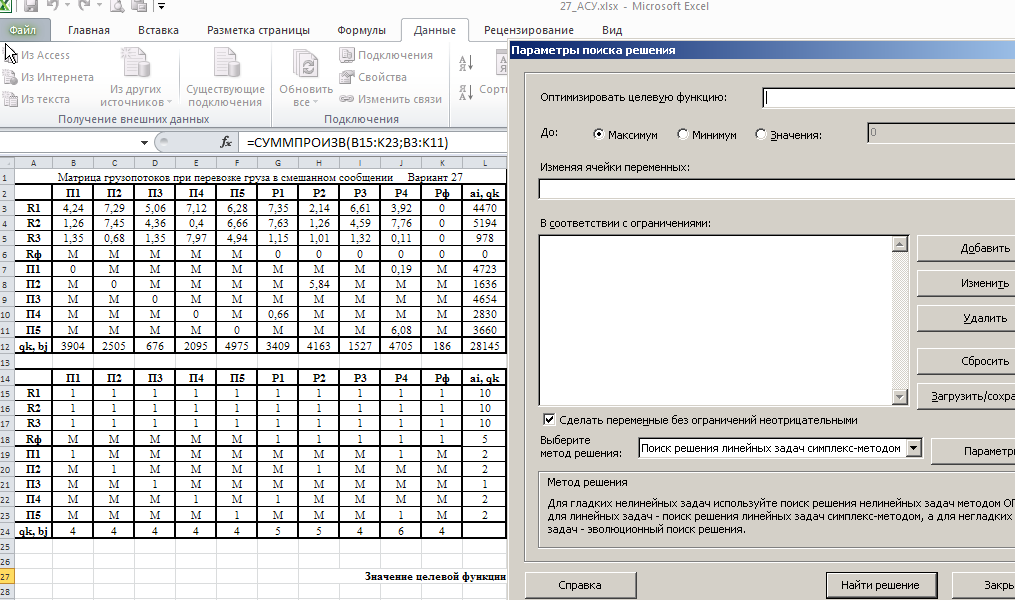 Рисунок 17 – Результат открытия приложения «Поиск решения» 2.12 В приложении «Поиск решения» выполняем следующие операции: 2.12.1 Указываем: адрес ячейки с введенной формулой для расчёта целевой функции; что оптимизация производится до минимального значения целевой функции [Рисунок 18]. 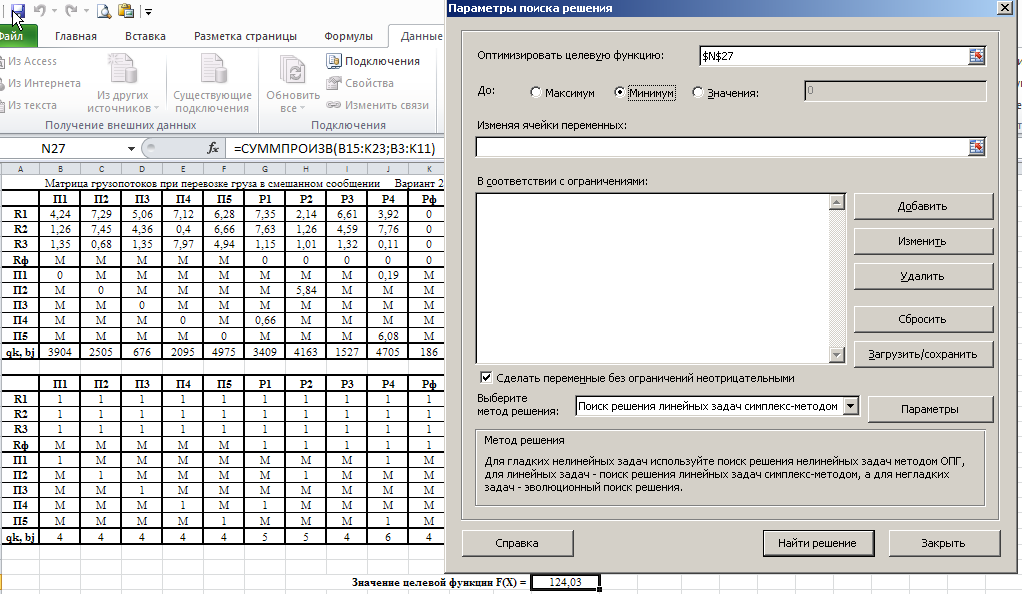 Рисунок 18 – Результат ввода в приложении «Поиск решения» адреса ячейки с целевой функцией и активация минимального значению целевой функции 2.12.2 Указываем, с какими ячейками производить манипуляции при поиске минимального значения целевой функции (в соответствующей ячейке с нажатой клавишей «Ctrl» перебираем все единицы второй матрицы) [Рисунки 19]. 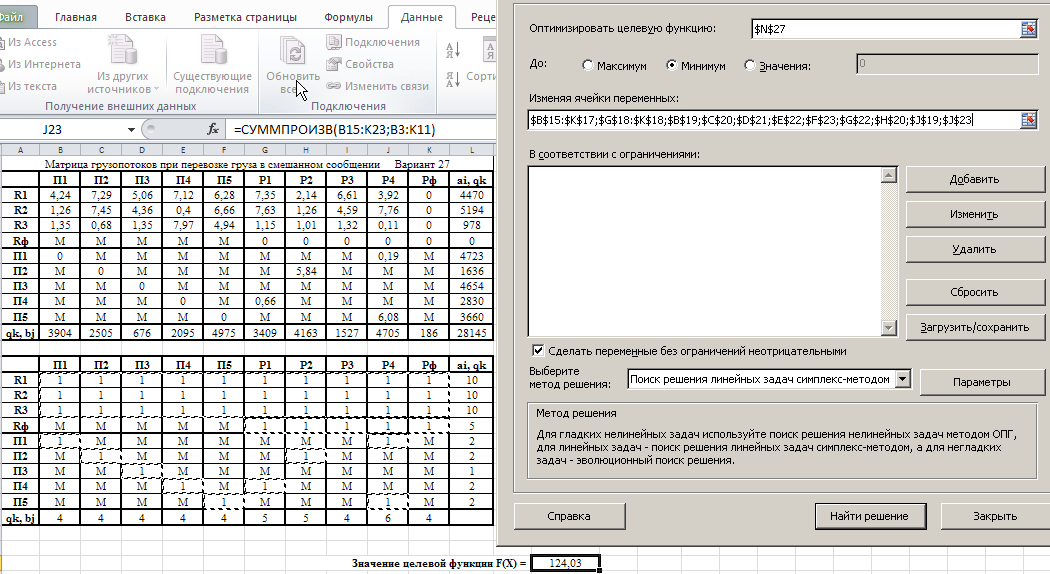 Рисунок 19 – Результат ввода ячеек, с какими производятся манипуляции при поиске минимального значения целевой функции 2.12.3 Указываем, ограничения, которые необходимо соблюдать при поиске минимального значения целевой функции (приравниваем потребности потребителей второй и первой матриц, а также ресурсы поставщиков ) [Рисунки 20 - 23].  Рисунок 20 – Определение в приложении «Поиск решения» окна для ввода ограничений  Рисунок 21 – Ввод ограничения потребностей потребителей  Рисунок 22 – Ввод ограничения ресурсов поставщиков  Рисунок 23 – Результат ввода ограничений, которые необходимо соблюдать при поиске минимального значения целевой функции 2.12.4 Открываем в приложении «Поиск решения» окно «Параметры». В окне «Параметры» устанавливаем: предельное количество итераций 1000, устанавливаем линейную модель оптимизации и ограничиваем интервал оптимизации неотрицательными значениями [Рисунок 24]. 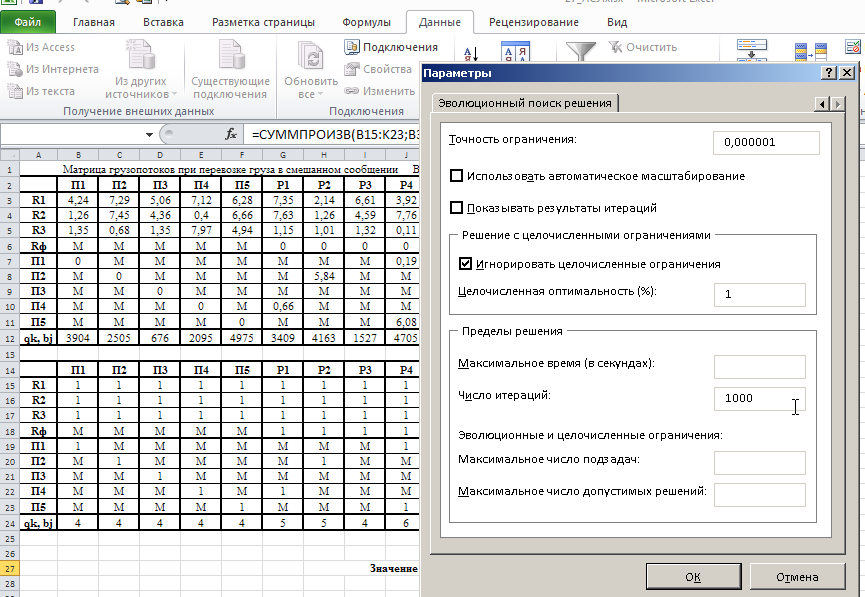 Рисунок 24 – Результат открытия в приложении «Поиск решения» окна «Параметры», установки предельного количества итераций, линейной модели оптимизации и ограничения интервала оптимизации неотрицательными значениями. 2.12.5 В окне «Параметры» нажимаем «кнопку» «ОК». 2.12.6 Для активации программы расчёта приложении «Поиск решения» нажимаем «кнопку» «Выполнить» 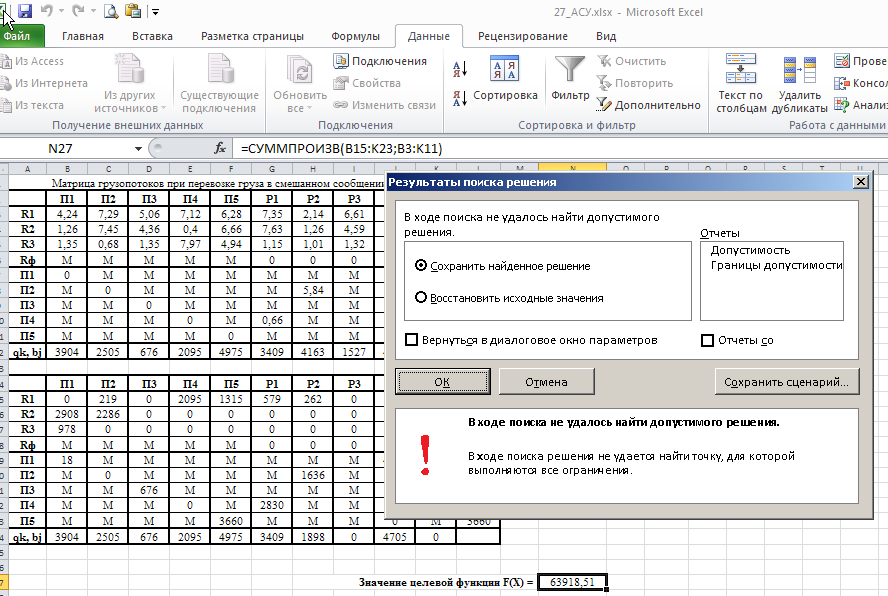 Рисунок 25 – Результат оптимизации Список используемых источников 1. «Оптимальное распределение перевозок в узле между тремя видами транспорта», рекомендации к выполнению курсовой работы по курсу: «Взаимодействие различных видов транспорта». Специальность: «Организация перевозок и управление на транспорте» (240100). Издание СибГГМА, Новокузнецк, 1996; 2. Правдин Н. В., Негрей В. Я., Подкопаев В. А. Взаимодействие различных видов транспорта: примеры и расчеты / Под ред. Н. В. Правдина. – М.: Транспорт, 1989. - 208 с. 3. Белов И. В., Каплан А. В. Математические методы в планировании на железнодорожном транспорте. – М.: Транспорт, 1972. – 248 с. |
