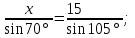Раздел
|
|
ФИО педагога
|
|
Дата
|
|
Класс
|
Количество присутствующих:
|
отсутствующих:
|
Тема урока
|
Решение треугольников
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
|
9.1.3.6 знать и применять теорему косинусов
9.3.3.7знать и применять теорему синусов
|
Цель урока
|
- знать теоремы косинусов и синусов;
- доказывать теоремы косинусов и синусов;
- применять теоремы для решения задач;
|
Ход урока
|
Этап урока
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Организационный момент.
|
Приветствует учеников. Для создания психологической атмосферы проводит игру «Путаница».
|
Проявление интереса к материалу изучения.
Ученики делятся на группы. Осмысливают поставленную цель.
|
|
|
Актуализация опорных знаний.
|
1. Отработка формул.
Найдите ошибку в ответе товарища:
1) а2 = в2 + с2 + 2вc cos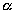
2) в2 = а2 + с2 – 2вс cos 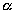
3) а2= а2 + с2 - 2ас sin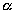
4)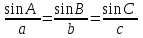
5) 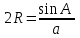
6) 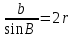
Тест на определение истинности (ложности) утверждения и правильности формулировок.
В треугольнике против угла в 150° лежит большая сторона.
В равностороннем треугольнике внутренние углы равны между собой и каждый равен 60°.
Существует треугольник со сторонами: 2 см, 7 см, 3 см.
Прямоугольный равнобедренный треугольник имеет равные катеты. (
Если один из углов при основании равнобедренного треугольника равен 50°, то угол, лежащий против основания, равен 90°.
Если острый угол прямоугольного треугольника равен 60°, то прилежащий к нему катет равен половине гипотенузы.
В равностороннем треугольнике все высоты равны.
Сумма длин двух сторон любого треугольника меньше третьей стороны.
Существует треугольник с двумя тупыми углами.
В прямоугольном треугольнике сумма острых углов равна 90°.
Если сумма двух углов меньше 90°, то треугольник тупоугольный.
|
Демонстрируют свои знания, умения по домашней работе
Сверяют ответы на слайде
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
И
|
И
|
Л
|
И
|
Л
|
И
|
И
|
Л
|
Л
|
И
|
И
|
|
Формативное оценивание
Устное оценивание
Самооценивание
|
Раздаточный материал
Слайд
|
Практическая работа. Решение задач на определение недоступных расстояний.
|
Задача 1. Для определения ширины непроходимого болота с вершины вертолета, находящегося на высоте h измерили углы α и β. Найти ширину болота АВ.
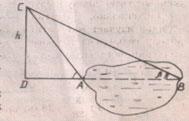
Дано: СD DВ;
<САВ = α; <СВD = β СD = h
Найти: АВ.
Решение: 1. Из прямоугольного треугольника АDC находим: АС = 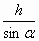
2. Из АВС по теореме синусов имеем:
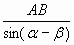 = = 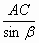 = = 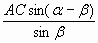 = = 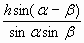
Ответ: 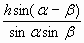
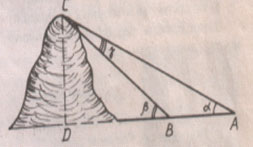
Дано: АВ = 200 м,
<САВ = α = 38°42’; СВD = β= 42°; СD DA.
Найти: СD.
Решение. 1. Из СВА по теореме синусов имеем равенство 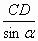 = = 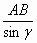 , откуда CB = , откуда CB = 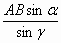 . .
2. Угол В — внешний угол АВС, поэтому β = α +γ, откуда γ = β – α.
3. СВ = 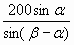 . .
4. Из СВD находим СD = СВ sinβ = 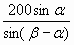 sinβ = 14325 м. sinβ = 14325 м.
Ответ: СD = 14 325 м.
|
Работают в группах
|
Устное оценивание
Взаимооценивание
|
Слайд
|
Индвидуальное работа
Решение задач
|
Работа по готовым чертежам
№ 1 1
а) Решение: 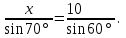 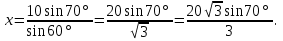
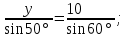 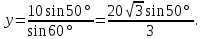
Ответ: 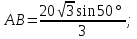 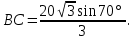
в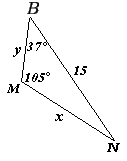 ) Решение: ) Решение: 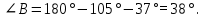
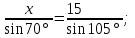
|
Решение задач демонстрируют на доске с проверкой на слайде
|
Самооценивание
|
Слайд
|
Рефлексия
|
Рефлексия:
Я активно/не активно участвовал в процессе урока
Доволен работой на уроке/необходимо поработать еще
Задания на уроке были понятны/ необходимо разобрать еще раз
|
|
|
|
Итог урока
|
Итак, наш урок подошел к концу.
- Какие цели мы ставили в начале урока? Достигли их?
|
Учащиеся подытоживают свои знания по изучаемой теме.
|
|
|
 Скачать 76.58 Kb.
Скачать 76.58 Kb.
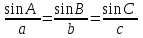
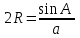
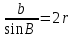


 1
1 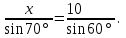
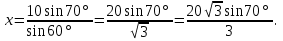
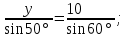
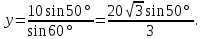
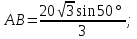
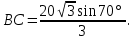
 ) Решение:
) Решение: