|
|
урок 45. Геометрия 9 класс. Решение треугольников
Раздел
|
Решение треугольников
|
ФИО педагога
|
|
Дата
|
|
Класс
|
Количество присутствующих:
|
отсутствующих:
|
Тема урока
|
Решение треугольников
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
|
9.1.3.9 знать и применять формулы для нахождения радиуса окружности, используя площади вписанных и описанных треугольников
|
Цель урока
|
Все учащиеся знают формулы для нахождения радиуса окружности, используя площади вписанных и описанных треугольников;
Большинство учащихся умеют применять формулы для нахождения радиуса окружности, используя площади вписанных и описанных треугольников;
Некоторые уащиеся могут решать задачи сложного уровня на нахождение радиуса окружности, используя площади вписанных и описанных треугольников;
|
Критерии успеха
|
Знать формулы для нахождения радиуса окружности, используя площади вписанных и описанных треугольников
Уметь применять формулы для нахождения радиуса окружности при решении задач
|
Ход урока
|
Этапы урока
|
Деятельность учителя
|
Деятельность обучающихся
|
Оценивание
|
Ресурсы
|
Орг. момент
|
Организационный момент. Приветствует учащихся, проверяет готовность к уроку, желает успеха. Учитель объявляет тему урока, учащиеся формулирует цели урока. Учитель корректирует их ответы.
Заполняют таблицу ЗХУ. В столбце «Знаю» пишут все, что они знают по теме урока; в столбце «Хочу узнать» пишут все, что им хотелось бы узнать по теме урока (с учетом цели урока). Последний столбец «Узнал» заполнят в конце урока.
|
Настраиваются на положительный настрой урока.
Формулируют цель урока
Заполняют таблицу ЗХУ
|
Комментарии учителя
|
Интерактивная доска
|
Закрепление изученного материала
|
Актуализация опорных знаний:
Проверка домашнего задания. Заранее перед уроком «дежурные» ученики на доске записывают ход решения домашних задач. В начале урока учитель вызывает трех учеников ( по количеству задач домашнего задания) для того, чтобы те объяснили ход решения. Остальные учащиеся слушают, задают вопросы и оценивают их ответ.
Тест
1.Окружность можно вписать в любой треугольник?
А) да, в любой. В) только в равносторонний. С) только в равнобедренный. Д) только в прямоугольный. Е) в треугольник нельзя вписать окружность.
2. В равносторонний треугольник со стороной 8 см вписана окружность. Чему равен радиус окружности?
А) 8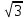 см В) 4 см В) 4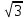 см С) 8 см Д) см С) 8 см Д) 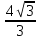 см Е) 2 см см Е) 2 см
3.Катеты прямоугольного треугольника равны 5 и 12. Чему равен радиус вписанной окружности.
А) 2. В) 4. С) 3. D) 2,5. E) 1.
4.Катеты прямоугольного треугольника относятся как 3 : 4. Периметр треугольника равен 24 см. Найдите радиус описанной окружности.
А) 5 см. В) 8 см. С) 6 см. D) 10 см. E) 12 см.
5.Сторона треугольника равна 10 см, а противолежащий угол 150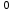 . Найдите радиус описанной окружности. . Найдите радиус описанной окружности.
А) 5 см. В) 10 см. С) 10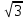 см. D) см. D) 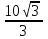 см. E) 5 см. E) 5 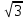 см. см.
Ответы:
А 2. Д 3. А 4. А 5. В
Критерии оценивания:
5 баллов – «Отлично»
4 балла – «Хорошо»
3 балла – «Старайся»
2 и ниже балла – «Учись решать задачи»
Решите задачи
Ученики самостоятельно обдумывают ход решения задач. Затем по желанию выходят к доске и решают у доски.
Задача 1.
П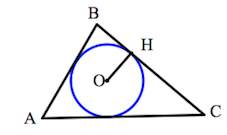 лощадь треугольника равна 800, а радиус вписанной окружности равен 16. Найдите периметр этого треугольника. лощадь треугольника равна 800, а радиус вписанной окружности равен 16. Найдите периметр этого треугольника.
Задача 2.
Н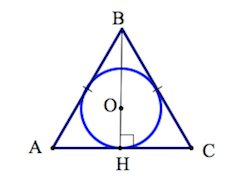 айдите радиус окружности, вписанной в правильный треугольник, высота которого равна 66. айдите радиус окружности, вписанной в правильный треугольник, высота которого равна 66.
Задача 3.
О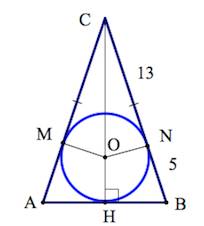 кружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 5, считая от вершины, противолежащей основанию. Найдите периметр треугольника. кружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 5, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Задача 4.
Р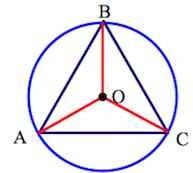 адиус окружности, описанной около правильного треугольника, равен 17 адиус окружности, описанной около правильного треугольника, равен 17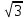 Найдите сторону этого треугольника. Найдите сторону этого треугольника.
З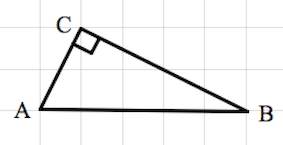 адача 5. адача 5.
Найдите радиус окружности, описанной около прямоугольного треугольника АВС, если стороны квадратных клеток равны 1.
Решения задач
Задача 1.
Задача проста, если знать формулу S= p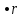 , где r – радиус вписанной в треугольник окружности, p – полупериметр треугольника. , где r – радиус вписанной в треугольник окружности, p – полупериметр треугольника.
800= p•16
p=50
Тогда P = 2p= 100
Ответ: 100.
Задача 2.
Радиус вписанной окружности в правильный треугольник OH – есть 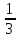 высоты BH, так в правильном треугольнике высоты совпадают с медианами, а медианы в точке пересечения делятся в отношении 2:1, считая от вершины. высоты BH, так в правильном треугольнике высоты совпадают с медианами, а медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
Итак, r = 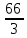 =22 =22
Ответ: 22.
Задача 3.
По свойству отрезков касательных, проведенных из одной точки к окружности, CM=CN=13, а поскольку H – середина AB, то AH=AM=BH=BN=5
P= 18+18+10= 46
Ответ: 46.
Задача 4.
Воспользуемся формулой 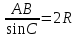 (т. Синусов); (т. Синусов);
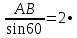 17 17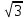
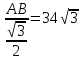
AB= 51
Ответ: 51.
Задача 5
В прямоугольном треугольнике центр описанной окружности – середина гипотенузы. Радиус описанной окружности равен половине гипотенузы.
R = 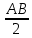 = 2.5 = 2.5
Ответ: 2,5.
|
Самостоятельно выполняют тест в тетрадях
|
Словесная оценка учителя.
Прием «Большого пальца»
Самопроверка по образцу
Словесная оценка учителя.
Выставляют баллы на полях тетради
|
Интерактивная доска
ИКТ
Раздаточный материал
Презентация
|
Подведение итогов урока (5 мин)
|
Итог урока. Рефлексия
Оцените свою работу на уроке
 Я доволен собой, у меня все получилось. Я доволен собой, у меня все получилось.
 У меня не все получилось, нужно повторить. У меня не все получилось, нужно повторить.
 Многое не получилось, нужно повторить Многое не получилось, нужно повторить
Домашнее задание:
Повторить формулы
Решить задачи:
1. К окружности, вписанной в треугольник АВС, проведены три касательных. Периметры полученных треугольников равны 6, 8. 10. Найдите площадь данного треугольника.
2. Сторона правильного треугольника равна 5. Найдите радиус вписанной окружности.
3. Сторона треугольника равна 1, противолежащий к этой стороне угол равен 300. Найдите радиус описанной окружности.
4. Боковая сторона равнобедреннего треугольника равна 40, а основание – 48. Найдите радиус описанной окружности.
|
Ученики показывают умение обосновывать свое понимание
Записывают д.з. в дневники
|
Самооценивание
|
Рефлексивный лист, стикеры
презентация
| |
|
|
 Скачать 143.97 Kb.
Скачать 143.97 Kb.