Документ Microsoft Word (2). Решение Угловую скорость вращения найдем, продифференцировав функцию зависимости угла поворота от времени (t) 1 0,13t 2

• Название: Решение Угловую скорость вращения найдем, продифференцировав функцию зависимости угла поворота от времени (t) 1 0,13t 2
• Дата: 17.04.2022
• Размер: 62.3 Kb.
• Имя файла: Документ Microsoft Word (2).docx
• Тип: Решение; #480268

1 (106.)

Диск радиусом R = 0,2м вращается согласно уравнению φ = 3- t + 0,l t ³ (угол в радианах, время в секундах). Определить тангенциальное аτ , нормальное an и полное a ускорения точек на окружности диска для момента времени t = 10с.

Дано: R = 0,2м

φ = 3- t + 0,l t ³

Решение: Угловую скорость вращения найдем, продифференцировав функцию зависимости угла поворота от
времени:
ω(t)= −1 +0,1*3*t^2.
Угловое ускорение вращения найдем, продифференцировав функцию зависимости угловой скорости
от времени:
β(t)= 0,6*t.
Числовые значения для времени t=10 с:
ω= 29, β= 6.
Нормальное ускорение an = r* ω^2
an = 0,2* 841= 168,2
Тангенциальное ускорение:
at = β/r,
at = 6/0,2 =30.
Полное ускорение:
a = (at^2 + an^2)^(0,5) = 170,85 (м/с^2).

Ответ: 170,85 (м/с²).
2(116). На нити висит груз массой 1,6 кг. На груз подействовала сила, действующая в горизонтальном направлении, величиной 12 Н. Найти силу натяжения нити в отклоненном состоянии груза.

Дано:

 кг - груз, висящий на нити;

 Н - сила, с помощью которой груз отводится в новое положение, действующая в горизонтальном направлении;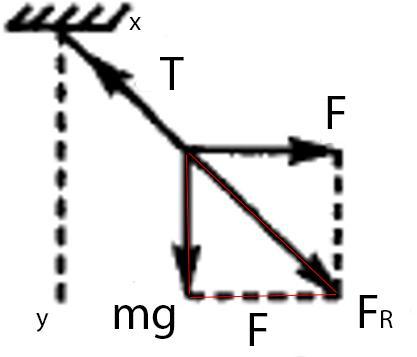



Найти  .

Решение:

Так как груз находится в покое, то приложенную горизонтальную силу, а также силу тяжести, действующую на груз, должна уравновешивать сила натяжения нити. В нашем случае сила натяжения нити является равнодействующей.

Поэтому согласно рисунку во вложении, нам необходимо вычислить модуль векторной суммы сил тяжести   и и горизонтальной силы  , перпендикулярных друг другу. Для этого достраиваем до "треугольника", добавляя проекцию силы натяжения нити в виде силы, равной  .

И чтобы найти третью сторону "треугольника", то есть равнодействующую  , необходимо согласно теореме косинусов, извлечь квадратный корень из разности суммы квадратов известных сторон и удвоенного произведения этих сторон на косинус угла между ними:



В нашем случае,  , это сила тяжести  , а   есть горизонтальная сила, приложенная к грузу:  . Косинус между ними будет равен 90 градусам, так как сила тяжести направлена всегда вертикально вниз, а сила

Поэтому получаем:



Косинус 90 градусов равен 0, тогда можем упростить нашу формулу:



 Н.

Ответ:20 н.

3(176). Материальная точка массой m = 0,1 г колеблется согласно уравнению x = 5sin20t (длина в сантиметрах, время в секундах). Определить максимальные значения возвращающей силы Fmax и кинетической энергии точки.

Дано: x=5sin20t, m = 0,1г = 10^–4кг.

Найти: F_max

Решение:
Из уравнения движения видим, что циклическая частота ω=20 1/с,
амплитуда А=5см=5*10^–2м.
Сила, под действием которой точка массы m совершает гармоническое колебание, равна
F =m*a
Ускорение точки a, совершающей колебание, равно
(d²/dt²)*x = –5*10^–2м*400/c²*sin(20t).
Ускорение будет максимально при sin(20t) = –1. aмакс= 5*10^–2м*400/c² = 20м/с²
Тогда максимальная сила F_макс = m*a_макс =10^–4кг *20м/с²= 0,002Н =2мH.
Полная энергия колеблющейся точки определяется уравнением:
W = ω²/2*A²*m =200/c²*(5*10^–2м) ²*10^–4кг = 200/c²*25*10^–4м²*10^–4кг =
= 0,5*10^–4Дж

4(206). Определить массу m1 одной молекулы сероуглерода CS2 принимая, что молекулы в жидкости имеют шарообразную форму и расположены вплотную друг к другу. Определить порядок величины диаметра d молекулы

Решение:

m0 = Mr(CS2)/N(a)
N(a) = 6 * 10^23 моль^-1
Mr(CS2) = 12 + 32 * 2 = 76 г/моль
m0 = 76/6*10^23 = 1,3 * 10^-22г.

Ответ: 1,3 * 10^-22г

5(256). Из баллона, содержащего водород под давлением Р1 = 10 атм при температуре t = 18° С, выпустили половину находившегося в нем количества газа, Считая процесс адиабатическим, определить конечную температуру t2 и давление Р2

Дано: p= 10⁶ Па

t = 18°С

ν₂ = ν/2

Найти: t₂ ― ?

p₂ ― ?

Решение: Абсолютная температура газа T = t+273 = 18+273 = 291 K.

Запишем уравнение Менделеева-Клапейрона для начального и конечного состояния газа:





где V ― объем баллона,

ν ― начальное количество молей газа,

R = 8,31 Дж/(К∙моль) ― молярная газовая постоянная,

Т и T₂ ― начальная и конечная термодинамическая температура газа.

Разделим почленно одно уравнение на другое:







Так как процесс адиабатический, для параметров газа выполняется равенство



где в левой части описано состояние половины газа (той половины, которая останется в баллоне после того, как вторая половина будет выпущена из баллона). γ = (i+2)/i ― постоянная адиабаты. i ― число степеней свободы молекулы. Для двухатомной молекулы водорода i = 5.

После сокращения на и с учетом (1) получим







Из уравнения (1):



Ответ: t₂ = –90 °C; p₂ = 0,31 МПа.

6(306). На продолжении оси тонкого прямого стержня равномерно заряженного с линейной плотностью заряда τ = 1,5нКл/см на расстоянии a = 12см от конца стержня находится точечный заряд q = 0,2 мкКл. Второй конец стержня уходит в бесконечность. Определить силу взаимодействия стержня и точечного заряда

Дано: τ = 1,5нКл/см

a = 12см

q = 0,2 мкКл

Найти F =?

Решение

Поскольку заряды являются одноименными, то взаимодействие носит характер отталкивания, причем, очевидно, что силы взаимодействия направлены вдоль линии стержня. Для определения величины силы поместим точечный заряд в начало координат и направим ось Ох вдоль стержня. Далее выделим на стержне элемент dx, расположенный на расстоянии х от точечного заряда. Заряд выделенного элемента dq = t dx, где t(тау) - линейная плотность заряда, можно считать точечным. Сила взаимодействия двух точечных зарядов q и dq определится согласно закону Кулона:
dF = k q dq/x^2, где k = 9*10^9 Н м^2/ Кл^2. Имеем:
dF = k q t dx/x^2.
Полная сила взаимодействия определится интегрированием по всей длине стержня, т.е. в пределах от d до бесконечности. Интегрирование функции 1/x^2 дает - 1/x, следовательно, в указанных пределах получим 1/d.
Таким образом, искомая сила взаимодействия определяется выражением:
F = k q t/d.
Выполним расчет:
F = 9*10^9*0.2*10^-6*1.5*10^-7/0.12 = 2.25*10^-3 Н.
7(33). Два прямолинейных длинных проводника расположены параллельно на расстоянии d1 = 10см друг от друга. По проводникам текут токи I1 = 20А и I2 = 30А в одном и том же направлении. Какую работу нужно совершить (на единицу длины проводника), чтобы раздвинуть эти проводники до расстояния d2 = 20см?

Дано d₁ = 10 см = 0,1 м

I₁ = 20 А

I₂ = 30 А

d₂ = 20 см = 0,2 м
Найти A_? - ?

Решение

Если по проводникам текут токи в одном направлении,

то проводники притягиваются и  необходимо совершить                   

работу против электромагнитных сил притяжения                  

  

Сила, действующая на единицу длины               

   

Работу вычисляем по формуле для работы переменной силы             

       

        

 

Ответ: 

8(406). На пластинку со щелью, ширина которой а = 0,05мм, падает нормально луч под углом α = 0,7мкм. Определить угол φ отклонения лучей, соответствующих первому дифракционному максимуму.

9(416). Определить угол θ расстояния фотона, испытавшего соударение со свободным электроном, если изменение длины волны при рассеянии Δλ = 0,363Å.

10(506). Оценить с помощью соотношения неопределённостей минимальную кинетическую энергию Тмин электрона, движущегося внутри сферической области диаметром l = 1Å.