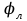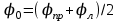лабораторная работа№9 Определение Определение модуля кручения нити и момента инерции системы, совершающей крутильные колебания. 9лаба. Лабораторная работа 9 Определение модуля кручения нити и момента инерции системы, совершающей крутильные колебания
 Скачать 345.82 Kb. Скачать 345.82 Kb.
|
|
Министерство науки и высшего образования Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова Кафедра физики  Дисциплина физика Лабораторная работа № 9 Определение модуля кручения нити и момента инерции системы, совершающей крутильные колебания
Санкт-Петербург 2022 г. Определение модуля кручения нити и момент инерции системы, совершающей крутильные колебания Цель работы – изучить законы динамики вращательного движения твердого тела и законы сохранения момента импульса и энергии; определить момент инерции крутильного маятника и модель кручения нити по результатам исследования неупругого соударения математического и крутильного маятников. Приборы и принадлежности: крутильный маятник, математический маятник, секундомер. Описание и принцип работы экспериментальной установки: 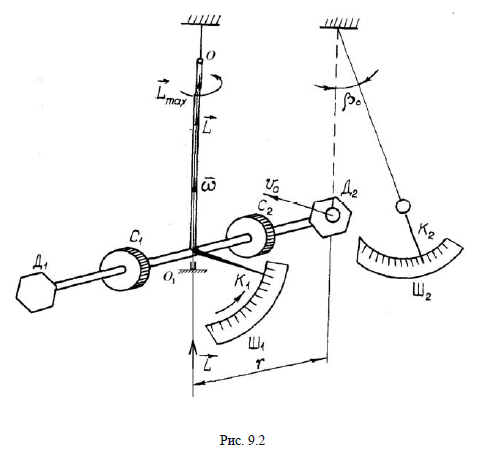 На горизонтальном стержне, кроме дисков Д, имеются цилиндры С, положение которых можно менять, передвигая их вдоль стержня (см. рис. 9.2). Изменение положений цилиндров С относительно оси вращения крутильного  маятника приводит к изменению момента инерции всей системы. К центру горизонтального стержня прикреплён указатель К1, при помощи которого можно измерять углы поворота ф крутильного маятника. Указатель К1 перемещается по шкале Ш1, проградуированной в градусах. Крутильный маятник, как уже было отмечено выше, состоит из двух взаимно перпендикулярных стержней. Вертикальный стержень подвешен на упругой нити, модуль кручения которой требуется определить экспериментально. Что касается теоретического значения модуля кручения, то, согласно теории упругих деформаций, для проволоки круглого сечения радиуса R и длины L модуль кручения равен: маятника приводит к изменению момента инерции всей системы. К центру горизонтального стержня прикреплён указатель К1, при помощи которого можно измерять углы поворота ф крутильного маятника. Указатель К1 перемещается по шкале Ш1, проградуированной в градусах. Крутильный маятник, как уже было отмечено выше, состоит из двух взаимно перпендикулярных стержней. Вертикальный стержень подвешен на упругой нити, модуль кручения которой требуется определить экспериментально. Что касается теоретического значения модуля кручения, то, согласно теории упругих деформаций, для проволоки круглого сечения радиуса R и длины L модуль кручения равен: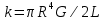 , где G - модуль сдвига материала проволоки. Математический маятник представляет собой шарик известной массы m, подвешенный на лёгком стержне длиной l. С шариком закреплен указатель К2, перемещающийся по вертикальной шкале Ш2, по которой определяются углы отклонения шарика от положения равновесия: , где G - модуль сдвига материала проволоки. Математический маятник представляет собой шарик известной массы m, подвешенный на лёгком стержне длиной l. С шариком закреплен указатель К2, перемещающийся по вертикальной шкале Ш2, по которой определяются углы отклонения шарика от положения равновесия: 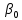 и и 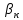 . Крутильный и математический маятники расположены так, что выведенный из положения равновесия шарик ударяется о диск крутильного маятника в то момент, когда скорость шарика направлена строго горизонтально. . Крутильный и математический маятники расположены так, что выведенный из положения равновесия шарик ударяется о диск крутильного маятника в то момент, когда скорость шарика направлена строго горизонтально. Основные формулы: Формула для расчёта момента инерции - 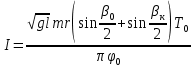 Формула для расчета модуля кручения нити - 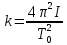 Формула для расчета модуля сдвига материала проволоки - 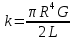 Ход работы: Цилиндры вплотную к дискам 1.  10 10
Цилиндры вплотную к вертикальному стержню крутильного маятника  10 10
2. 1) Iср= 2.03 - расчёт среднего значения момента инерции для таблицы измерений при цилиндрах вплотную к дискам. k=2.465 – расчёт модуля кручения нити для таблицы измерений при цилиндрах вплотную к дискам. 2) Iср= 1.046 - расчёт среднего значения момента инерции для таблицы измерений при цилиндрах вплотную к вертикальному стержню крутильного маятника. k=1.508 - расчёт модуля кручения нити для таблицы измерений при цилиндрах вплотную к вертикальному стержню крутильного маятника. 3. 4. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

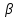 K
K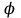 пр
пр