задачи по физике. Задача 1,2. Решение Уравнение гармонических колебаний имеет вид x Asin(t) 0,15sin(t6) (1)

• Название: Решение Уравнение гармонических колебаний имеет вид x Asin(t) 0,15sin(t6) (1)
• Анкор: задачи по физике
• Дата: 16.09.2022
• Размер: 27.77 Kb.
• Имя файла: Задача 1,2.docx
• Тип: Решение; #680682

Задача 1. Материальная точка массой m совершает гармонические колебания по закону x = A ∙ sin(ωt+φ). Определить амплитудное значение скорости скорости v_m, максимальное значение силы F_m, действующей на точку, и ее полную энергию.

Вариант	m, кг	А, м	ω	φ
	0,10	0,20	π	π/6

Дано: m = 0,10 кг; А = 0,20м; ω = 9π; φ = π/2

Найти: v_m, F_m, W

Решение:

Уравнение гармонических колебаний имеет вид:

X = Asin(ωt+φ) = 0,15∙sin(πt+π/6) (1)

Взяв первую производную смещения по времени, найдем скорость колеблющейся точки:

υ = А ω ⋅ cosω ∙ t

Отсюда амплитудное значение скорости:

υ = А ω ⋅ cosω = 0,20 ∙ π ⋅ cos π = 0,63 м/с

Полная энергия колеблющейся точки равна максимальному значению ее кинетической энергии:

W = 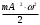= = 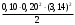0,02Дж = 20мДж

Согласно второму закону Ньютона

F = ma (2)

Ускорение колеблющейся точки найдем, взяв вторую производную смещения по времени (или, что то же самое, первую производную от скорости по времени) :

а =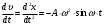

Отсюда максимальное ускорение: a_max = A ∙ ω² .

Подставив это выражение максимального ускорения в соотношение (2), найдем максимальную силу, действующую на точку:

F_max = m ⋅ A⋅ ω² = 0,10 ⋅ 0,20 ⋅ (3,14 )² = 0,197 Н

Проверка размерности:

[υ] = м ∙ с^-1 = м/с

[W] = кг ∙ м² /с² = Н ∙ м = Дж

[F] = кг ∙ м /с² = Н

Ответ: υ = 0,63 м/с; W = 20мДж; F_max = 0,197 Н.
Задача 2. Максимальное значение силы тока в колебательном контуре, состоящего из катушки индуктивности и конденсатора, равно I_m, максимальное значение напряжения на обкладках конденсатора равно U_m. Циклическая частота колебаний равна ω, если энергия контура равна W.

Определить величины, указанные в таблице знаком опроса.

Вариант	Im,А	Um, В	W, мДж	ω, с-1
	0,1	200	0,2	?

Дано:

I_m,=0,1 А; U_m = 200В; W = 0,2мДж = 0,2 ∙ 10^-3Дж

Найти: ω - ?
Решение:

Амплитуда колебаний напряжения на конденсаторе связана с амплитудой колебания заряда на его обкладках соотношением  

q_m = C ∙ U_m

С другой стороны, амплитуда колебаний тока в контуре связана с амплитудой колебания заряда соотношением 

I_m, = q_m ∙ ω

 Энергия контура:

W =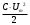

Откуда С =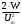

Объединяя эти равенства, для ω получаем:

ω =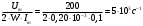

Проверка размерности:

[ω]= В / Дж ∙ А =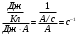

  Ответ: ω = 5 ·10³с^-1