решение уравнения в excel. уравнение. Решение уравнений

• Название: Решение уравнений
• Анкор: решение уравнения в excel
• Дата: 22.11.2022
• Размер: 57.5 Kb.
• Имя файла: уравнение.doc
• Тип: Решение; #806681

Решение уравнений

Аналитическое решение некоторых уравнений, содержащих, например тригонометрические функции может быть получено лишь для единичных частных случаев. Так, например, нет способа решить аналитически даже такое простое уравнение, как cos x=x

Численные методы позволяют найти приближенное значение корня с любой заданной точностью.

Приближённое нахождение обычно состоит из двух этапов:

1) отделение корней, т.е. установление возможно точных промежутков [a,b], в которых содержится только один корень уравнения;

2) уточнение приближённых корней, т.е. доведение их до заданной степени точности.

Мы будем рассматривать решения уравнений вида f(x)=0. Функция f(x)определена и непрерывна на отрезке [а.Ь]. Значение х₀ называется корнем уравнения если f(х₀)=0

Для отделения корней будем исходить из следующих положений:

• 
  Если f(a)* f(b] < 0 , то внутри отрезка \a, b\ существует, по крайней мере, один корень
  
• 
  Если функция y = f(x) непрерывна на отрезке [a, b], и f(a)*f(b)<0 и f'(x) на интервале (a, b) сохраняет знак, то внутри отрезка [а, b] существует единственный корень уравнения
  

Приближённое отделение корней можно провести и графически. Для этого уравнение (1) заменяют равносильным ему уравнением р(х) = ф(х), где функции р(х) и ф(х] более простые, чем функция f(x). Тогда, построив графики функций у = р(х) и у = ф(х), искомые корни получим, как абсциссы точек пересечения этих графиков

Метод дихотомии

Для уточнения корня разделим отрезок [а, b] пополам и вычислим значение функции f(х) в точке x_sr=(a+b)/2. Выбираем ту из половин [a,x_sr ] или [x_sr ,b], на концах которых функция f(x) имеет противоположные знаки.. Продолжаем процесс деления отрезка пополам и проводим то же рассмотрение до тех пор, пока. длина [a,b] станет меньше заданной точности. В последнем случае за приближённое значение корня можно принять любую точку отрезка [a,b] (как правило, берут его середину). Алгоритм высокоэффективен, так как на каждом витке (итерации) интервал поиска сокращается вдвое; следовательно, 10 итераций сократят его в тысячу раз. Сложности могут возникнуть с отделением корня у сложных функций.

Для приближенного определения отрезка на котором находится корень можно воспользоваться табличным процессором, построив график функции

ПРИМЕР: Определим графически корень уравнения . Пусть f1(х) = х, a и построим графики этих функций. (График). Корень находится на интервале от 1 до 2. Здесь же уточним значение корня с точностью 0,001(на доске шапка таблицы)

Решение в Excel,

Алгоритм для программной реализации

1. 
   а:=левая граница b:= правая граница
   
2. 
   m:= (a+b)/2 середина
   
3. 
   определяем f(a) и f(m)
   
4. 
   если f(a)*f(m)<0 то b:=m иначе a:=m
   
5. 
   если (a-b)/2>e повторяем , начиная с пункта2
   
   
   

Метод хорд.

Точки графика функции на концах интервала соединяются хордой. Точка пересечения хорды и оси Ох (х*) и используется в качестве пробной. Далее рассуждаем так же, как и в предыдущем методе: если f(x_a) и f(х*) одного знака на интервале , нижняя граница переносится в точку х*; в противном случае – переносим верхнюю границу. Далее проводим новую хорду и т.д.

О 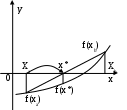сталось только уточнить, как найти х*. По сути, задача сводится к следующей: через 2 точки с неизвестными координатами (х₁, у₁) и (х₂, у₂) проведена прямая; найти точку пересечения этой прямой и оси Ох.

З апишем уравнение прямой по двум точках:



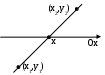В точке пересечения этой прямой и оси Ох у=0, а х=х*, то есть

, откуда

процесс вычисления приближённых значений продолжается до тех пор, пока для двух последовательных приближений корня х„ и х_п_1не будет выполняться условие abs(xn-x_n-1)<e, где е - заданная точность

Сходимость метода гораздо выше предыдущего

Алгоритм различается только в пункте вычисления серединной точки- пересечения хорды с осью абсцисс и условия останова (разность между двумя соседними точками пересечения)

Решение в Excel

Уравнения для самостоятельного решения: (отрезок в excel ищем самостоятельно)

1. 
   (х=1,261)
   
2. 
   (х=?)
   

3. 
   sin(x/2)+1=x^2 (х=1,26)
   

4. 
   y=sin3x*cos5x (х=?)
   
5. 
   (х=0,756)
   

6. 
   x-cosx=0 (х=0,739)
   

7. 
   x^2+4sinx=0 (х=-1,933)
   

8. 
   x=(x+1)³ (х=-2,325)